wektor jednostkowy
anonim123: Znajdź wektor jednostkowy dzielący na dwie równe połowy kąt pomiędzy wektorami
wektor a=[2,−2,2] b=[6,3,−6]
11 maj 16:02
wredulus_pospolitus:
A mogą być NIERÓWNE połowy

11 maj 16:28
wredulus_pospolitus:
Metoda 'na szybkiego' aka 'nie pamiętamy teorii'
Krok 1:
zaczepiamy wektory w (0,0,0)
Krok 2:
tworzymy wektory jednostkowe
Krok 3:
Z kroku 2 mamy współrzędne końców wektorów
Krok 4:
Wyznaczamy współrzędne połowy odcinka pomiędzy końcami tychże wektorów
Krok 5:
Z kroku 4 mamy wektor idący z punktu (0,0,0) do środka odcinka
Krok 6:
Robimy wektor jednostkowy
11 maj 16:31
anonim123: Dlaczego wektor d=wersor AB+wersor AC a nie wektor=wektor AB+ wektor AC
przez wektor d oznaczam przekątną?
11 maj 17:53
anonim123: wektor d=wektor AB+ wektor AC
11 maj 17:59
∑: na 2 to pryszcz, daj radę z 3 albo złotym podziałem
11 maj 18:08
anonim123: ?
11 maj 18:55
wredulus_pospolitus:
anonim zacznijmy od tego −−− na jakim poziomie nauczania jesteś

11 maj 19:16
anonim123: na studiach na mechatronice
11 maj 19:29
Mila:
Dobrze przepisane dane? Rachunki nieładne są.
11 maj 21:36
Mila:
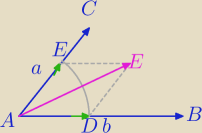
a=[2,−2,2] , b=[6,3,−6]
Przekątna rombu jest dwusieczną kąta.
Normalizujemy wektory a i b
|a|=
√22+22+22=
√12=2
√3
|b|=
√62+32+62=9
| | 1 | | −1 | | 1 | | √3 | | √3 | | √3 | |
a1=[ |
| , |
| , |
| ]=[ |
| ,− |
| , |
| } |
| | √3 | | √3 | | √3 | | 3 | | 3 | | 3 | |
| | √3+2 | | −√3+1 | | √3−2 | |
a1+b1=[ |
| , |
| , |
| ] |
| | 3 | | 3 | | 3 | |
| | √3+2 | | −√3+1 | | √3−2 | |
AE=[ |
| , |
| , |
| ] − wektor dwusiecznej |
| | 3 | | 3 | | 3 | |
Trzeba go znormalizować
| | √(√3+2)2+(1−√3)2+(√3−2)2 | | √18−2√3 | |
|AE|= |
| = |
| |
| | 3 | | 3 | |
Dokończ, wcześniej
posprawdzaj rachunki, może coś źle obliczyłam.
11 maj 23:17
anonim123: Dlaczego wektor d=wersor AB+wersor AC a nie wektor d=wektor AB+ wektor AC?
Nie znalazłam odpowiedzi na moje pytanie może ktoś wytłumaczyć?
12 maj 11:37
ICSP: Ponieważ kierunek dwusiecznej kąta wyznacza suma wersorów a nie wektorów.
12 maj 11:57
wredulus_pospolitus:
@anonim123 bo
d jest dwusieczną kąta, a nie przekątną.
Prosty przykład:
masz PROSTOKĄT o wymiarach 2 x 100
jak wyznaczysz DWUSIECZNĄ (czyli pod kątem 45
o poprowadzoną linię) ... nie będzie to przecież
przekątna tegoż prostokąta, prawda

A właśnie przekątną byś otrzymał, gdybyś brał do obliczeń wektory AB i AD tegoż prostokąta
12 maj 12:10
Mila:
Napisałam:
Przekątna rombu jest dwusieczną kąta między bokami.
Dopisuję: Przekątna podanego równoległoboku nie jest dwusieczną kata między bokami.
12 maj 17:03
anonim123: dzięki

12 maj 17:08


 a=[2,−2,2] , b=[6,3,−6]
Przekątna rombu jest dwusieczną kąta.
Normalizujemy wektory a i b
|a|=√22+22+22=√12=2√3
|b|=√62+32+62=9
a=[2,−2,2] , b=[6,3,−6]
Przekątna rombu jest dwusieczną kąta.
Normalizujemy wektory a i b
|a|=√22+22+22=√12=2√3
|b|=√62+32+62=9
 A właśnie przekątną byś otrzymał, gdybyś brał do obliczeń wektory AB i AD tegoż prostokąta
A właśnie przekątną byś otrzymał, gdybyś brał do obliczeń wektory AB i AD tegoż prostokąta
