równanie per: Rozwiąż równanie sinx * sin2x * sin3x + cosx *cos2x * cos3x=1.

6latek: najpierw rozpatrzmy sinx * sin2x * sin3x

	1
sinx*sin3x=		*cos2x−cos4x
	2

Teraz pytanie

	1
Jak policzyc sin2x*		(cos2x−cos4x)?
	2

Mozna by to zapisac sobie tak

1
	*sin2x(cos2x−cos4x)
2

Wiec bedziemy korzystac dalej ze wzoru na sinx*cosx ? czyli musimy policzyc sin2x*cos2x−sin2x−cos 4x?

	1
Potem jeszcze to domnozyc przez		?
	2

Jeszcze mam pytanie

	1
Jesli mam wzor sinα*cosβ=		[sin(α+β)+sin(α−β)] to czy gdy mama tak
	2

cosα*sinβ to po znaku rownosci moge napisac to samo? dziekuje za odpowiedzi

6latek: tam ma byc −sin2x*cos4x

ite: wtedy w nawiasie będzie wyrażenie [sin(α+β)+sin(β−α)] ← suma jest działaniem przemiennym a różnica nie jest

Ivona: https://www.wolframalpha.com/input/?i=sin%28x%29sin%282x%29sin%283x%29%2Bcos%28x%29cos%282x%29cos%283x%29%3D1

wredulus_pospolitus: jest to jakiś sposób ... problem w tym, że nie do końca się przybliżasz do sedna sprawy ... co prawda trochę (ale to trochę) porozdzielałeś ten iloczyn, ale wskakujesz na kąty: (2x), (4x) i (6x) ale zapewne da się to tak zrobić

6latek: Dziękuje . Po pracy zaraz sie tym zajme

6latek: Wredulus witaj. Chociaz moj problem to nic w porownaniu z tym co teraz bedzie sie dzialo na forum

Filip: Młody a cobedzie sie dziac? .....

kos: sin(2x)=2sinxcosx sin(3x)= sinx(3−4sin²x) cos(2x)=2cos²x−1) cos(3x)=cosx(4cos²x−3) i sin²x=1−cos²x podstaw cosx=t , t∊<−1,1> i otrzymasz równanie wielomianowe ze zmienną "t" ...................

Ile: kos jak podstawisz t i otrzymasz równanie wielomianowe

6latek: Filip myslalem ze beda wrzucane zadania z matury na forum .

Ile: Przecież są w pdf

per: Jak to rozwiązać w końcu

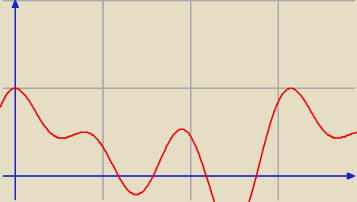
piotr: pezkształcając do postaci: 1/4 (1+Cos[2 x]+Cos[4 x]+Cos[6 x]+Sin[2 x]+Sin[4 x]−Sin[6 x])=1 od razu widać rozwiązanie: x=kπ teraz trzeba udowodnić, że to jedyne rozwiązanie

per: A jak wykazać że to jedyne rozwiązanie?

I'm back: Napisał @ktos w jaki sposób. Robisz podstawienie i rozwiazujesz równanie kwadratowe.

per: Ale tam są też sinusy a ktos pisze zeby podstawic za cosx, a co za sinx

I'm back: Przeczytaj uważnie co napisał. Zamieniasz sin²x na 1 − cos²x. Będa same cos²x i robisz podstawienie

per: I'm back sinx * sin2x * sin3x=sinx*2sinxcosx*sinx(3−4sin²x) jak przejść do samych cosinusów z tego oczywiście bez pierwiastków

chichi: 2sin(x)cos(x)*sin(x)(3−4sin²(x))=2[1−cos²(x)]*cos(x)*[3−4(1−cos²(x))]

per: Ok tylko nie wiem co z tym ostatnim nawiasem (t − 1) (t + 1) (8 t⁴ − 8 t³ − 2 t² + 2 t + 1)

per: Liczyć pochodną i badać przebieg zmienności?

6latek: A domnozyles to wszystko przez sinx ? Policzone jest sin2x*sin(3x)

per: Nie pomnożone jakoś mi umknęlo i co zrobić właśnie z tym sinx wiedziałem ze coś zostanie z tych sinusów

6latek: popelniam teraz bardzo duzo bledow wiec az boje sie liczyc no ale sprobuje sinx*sin(3x)= sinx*sinx(3−4sin²x)= sin²x(3−4sn²x) sin²x(3−4sin²x)*2sinx*cosx= 2sin³x(3−4*sin²x)*cosx =2sin²x(3−4sin²x)*sinx*cosx Ale naprawde dobrze sprawdz

per: Ok a jak to wkorzystać w takim razie

6latek: Teraz nalezaloby policzyc cosx*cos2x*cos3x i zobaczyc co dostaniemy z tego Moze wredlus pojawi sie na forum

per: Nie jestem wredny, tylko nie wiem jak to wykorzystać

6latek: Och. ja nie mowilem o Tobie .Wredulus_pospolitus to takze I'm back Jedynie co na teraz to z pierszego sin²x= 1−cos²x ale zostaje sinxcosx i tez za bardzo nie wiem co z tym zrobic Moze ktos inny

piotr: t=sinx t² (−7+2 t (3 Sqrt[1−t²]+t (7−4 t (t+Sqrt[1−t²]))))=0 t²=0 lub −49 + 232 t² − 440 t⁴ + 384 t⁶ − 128 t⁸=0 to równanie ma tylko zespolone pierwiastki

piotr: {{t = −0.781686 + 0.209642 I}, {t = 0.781686 − 0.209642 I}, {t = −0.781686 − 0.209642 I}, {t = 0.781686 + 0.209642 I}, {t = −0.968904 + 0.076538 I}, {t = 0.968904 − 0.076538 I}, {t = −0.968904 − 0.076538 I}, {t = 0.968904 + 0.076538 I}}

Mila: sinx * sin2x * sin3x + cosx *cos2x * cos3x=1⇔ sinx * sin2x * sin3x =1− cosx *cos2x * cos3x

	1
P=		[sin2x+sin2(2x)+sin2(3x)]
	2

L= sinx * sin2x * sin3x = dokończ 6−latku na podobna postać, po 20 znowu będę liczyć.

per: A co zrobić z lewą stroną, aby uzyskać coś podobnego?

Mila: To mam tak jak : 21:01 (sin2x+cos2x)+(sin4x+cos4x)+(cos(6x)−sin(6x))=3

per: Ok i Mila jak dalej?

per: Czy zniknął post

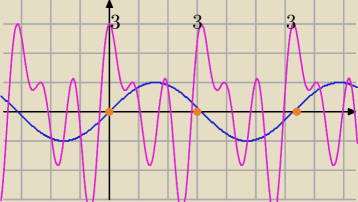
Mila: Teraz to raczej intuicja niż rachunki. x=kπ sinusy − 0 cosinusy 1 (sin2x+cos2x)+(sin4x+cos4x)+(cos(6x)−sin(6x))−3

Mila: Jutro coś wymyślę. Na pewno można porachować Skąd masz to zadanie?

Mila: sinx * sin2x * sin3x =1− cosx *cos2x * cos3x Przekształcam obie strony równania: 1)

	1
L=sinx * sin2x * sin3x=		*(2sinx*sin2x)*sin(3x)=
	2

	1
=		*[(cosx−cos3x)*sin3x]=
	2

	1
=		[sin3x*cosx−sin3x*cos3x]=
	2

	1
=		*[2sin3x*cosx−2sin3x*cos3x]=
	4

	1
=		*(sin4x+sin2x−sin6x)
	4

==================== 2)

	1
P=1−		*(2cosx*cos2x)*cos(3x)=
	2

	1
=1−		[(cosx+cos3x)*cos(3x)]=
	2

	1
=1−		*[cosx*cos3x+cos2(3x)]=
	2

	1
=1−		*[2cosx*cos3x+2cos2(3x)]=
	4

	1
=1−		*[cos2x+cos4x+1+cos(6x)]=
	4

	1		1		1		1
=1−		−		cos2x−		cos4x−		cos6x=
	4		4		4		4

	1
=−		*(−3+cos2x+cos4x+cos6x)
	4

========================= 3) otrzymuję równanie:

1		1
	*(sin4x+sin2x−sin6x)+		*(−3+cos2x+cos4x+cos6x)=0⇔
4		4

(sin2x+cos2x)+(sin4x+cos4x)+(cos6x−sin6x)=3 x=kπ To tyle na dzisiaj.

Mariusz: −2*(−49 + 232 t² − 440 t⁴ + 384 t⁶ − 128 t⁸=0) 256t⁸−768t⁶+880t⁴−464t²+98 = 0 Wielomian z tego równania można rozłożyć 256t⁸−768t⁶+880t⁴−464t²+98 = 0 y = t² 256y⁴−768y³+880y²−464y+98 =0 (256y⁴−768y³)−(−880y²+464y−98)=0 (256y⁴−768y³+576y²)−(−304y²+464y−98)=0 (16y−24y)²−(−304y²+464y−98)=0

	y		y2
(16y−24y+		)2−((16y−304)y2+(−24y+464)y+		−98)=0
	2		4

(y²−196)(16y−304)−(24y−464)²=0 y³−55y²+1196y−9732=0 Powyższe równanie można rozwiązać korzystając z podstawienia

	55
y=u+v+
	3

a następnie zapisując je w postaci układu równań który będzie przypominał wzory Vieta dla równania kwadratowego piotr czy ty samodzielnie to równanie rozwiązałeś ? czy wziąłeś rozwiązanie z jakiegoś programu To równanie dałoby się rozwiązać ale sporo byłoby liczenia no i bez texa nie dałoby się porządnie tych pierwiastków zapisać

Mariusz: Po sprowadzeniu do tangensa otrzymałem takie równanie

	(tg4(x)+2tg3(x)−6tg(x)+7)tg2(x)
−		=0
	(1+tg2(x))3

tg⁴(x)+2tg³(x)−6tg(x)+7=0 y⁴+2y³−6y+7=0 (y⁴+2y³)−(6y−7)=0 (y⁴+2y³+y²)−(y²+6y−7)=0 (y²+y)²−(y²+6y−7)=0

	w		w2
(y2+y+		)2−((w+1)y2+(w+6)y+		−7)=0
	2		4

(w²−28)(w+1)−(w+6)²=0 (w³+w²−28w−28)−(w²+12w+36)=0 w³−40w−64=0 w=u+v u³+3u²v+3uv²+v³−40(u+v)−64=0

	40
u3+v3−64+3(u+v)(uv−		)=0
	3

u³+v³=64

	40
uv=
	3

u³+v³=64

	64000
u3v3=
	27

	64000
t2−64t+		=0
	27

	64000
(t−32)2−1024+		=0
	27

	64000−27648
(t−32)2+		=0
	27

	36352
(t−32)2+		=0
	27

i aby dalej liczyć trzeba by użyć liczb zespolonych bądź wrócić do równania w³−40w−64=0 i skorzystać z trygonometrii

piotr: pierwiastki policzyła: https://www.wolframcloud.com/obj/cae13ec0-5bbb-4f66-98c6-c31de0fcb71f

per: Ale nie ma na to innego sposobu z wzorami trygonometrycznymi tylko ?