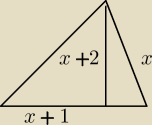
trójkąt Nel: Pewien trójkąt ma boki o długościach: 𝑥, 𝑥 + 1, 𝑥 + 2 gdzie 𝑥 > 3. Wysokość poprowadzona na bok o długości 𝑥 + 1 dzieli ten bok na dwa odcinki. Wykaż, że jeden z tych odcinków jest o 4 dłuższy od drugiego

Szkolniak: Z twierdzenia Pitagorasa: t²+h²=x² oraz (x+1−t)²+h²=(x+2)² h²=x²−t² oraz h²=(x+2)²−(x+1−t)² Porównujemy h²: x²−t²=(x+2)²−(x+1−t)² x²−t²=(x+2+x+1−t)(x+2−x−1+t) x²−t²=(2x+3−t)(t+1) x²−t²=2xt+2x+3t+3−t²−t x²=2xt+2x+2t+3 x²−2xt−2x−2t−3=0 x²−1−2xt−2x−2t−2=0 (x²−1)−2xt−2t−2x−2=0 (x²−1)−2t(x+1)−2(x+1)=0 (x+1)(x−1)−2t(x+1)−2(x+1)=0 (x+1)(x−1−2t−2)=0 (x+1)(x−2t−3)=0 x=−1 v x=2t+3 Oczywiście przypadek x=−1 odpada, bo x>3. Zostaje x=2t+3. Nasze długości tych dwóch odcinków wynoszą więc u nas: t oraz x+1−t t oraz 2t+3+1−t t oraz t+4 Stąd widzimy że jeden odcinek jest o 4 dłuższy od drugiego, cnw.

Jolanta: zrobiłam wprowadzając wysokośc h i a+b=x+1 a+b=x+1 a²+h²=(x+2)² i b²+h²=x² h²=(x+2)²−a² h²=x²−b² (x+2)²−a²=x²−b² x²+4x+4−x²=a²−b² 4(x+1)=(a+b)(a−b) 4(a+b)=(a+b)(a−b) 4=a−b