geometria analityczna rozszerzenie: Punkty A=(3,9), B=(−5,3) oraz C=(2,−6 1/3) są kolejnymi wierzchołkami czworokąta opisanego na okręgu o środku w punkcie S=(2,2). Wyznacz współrzędne wierzchołka D.

Mariusz: Sporządziłem rysunek w Geogebrze i oto co wyszło https://prnt.sc/12p0h5i

chichi: @Mariusz no fajnie i co dalej?

Mariusz: Z rysunku wynikałby taki plan działania 1. Znaleźć promień okręgu 2. Napisać równania stycznych do okręgu przechodzących przez punkty A oraz C 3. Rozwiązać układ równań liniowych aby znaleźć punkt D

chichi: Z GeoGebrą świat staje się piękniejszy

Mariusz: @chichi jak masz lepszy pomysł to podziel się nim Ja takie zadania rozwiązywałem ponad 20 lat temu

chichi: @Mariusz tu nie chodzi o to, że ja widzę coś złego w Twoim sposobie rozwiązywania tego zadania, on mi się bardzo podoba, tylko pamiętaj, że żyjemy w Polsce, w której wciąż na maturze obowiązuje kalkulator prosty...

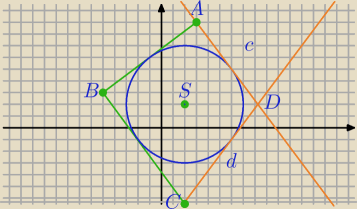
Mila: A=(3,9), B=(−5,3) oraz C=(2,−6 1/3) 1) prosta AB: 9=3a+b i −3=−5a+b =============

	3		27
a=		, b=
	4		4

	3		27
y=		x+		/*4
	4		4

AB: 3x−4y+27=0 =========== 2) Odległość Punktu S od prostej AB:

	|3*2−4*2+27|		25
D(S,pr.AB)=		=		=5
	√32+42		5

r=5 3) Prosta CD: D=(x,y)

	19		19
y=ax+b i −		=2a+b, b=−		−2a
	3		3

	19		19
d: y=ax−		−2a⇔ d: ax−y−		−2a=0
	3		3

Odległość punktu S od prostej CD równa 5

	19   |2a−2− −2a|   3
D(S,d)=		=5
	√a2+1

	19
|2+		|=5*√a2+1 /2
	3

	25		25
(		)2=25(a2+1) ⇔		=a2+1
	3		9

25=9a²+9 ⇔9a²=16

	16		4		4
a2=		⇔ a=		lub a=−		⇒Prosta BC⊥AB
	9		3		3

	4
d: y=		x−9
	3

========== 4) Prosta AD: y=ax+b i 9=3a+b, b=9−3a y=ax+9−3a⇔ c: ax−y+9−3a=0

	|2a−2+9−3a|
d(S,c)=5=
	√a2+1

5√a²+1=|7−a| /² 25a²+25=49−14a+a² 24a²+14a−24=0 12a²+7a−12=0

	4		3
a=−		lub a=		to wsp. prostej AB
	3		4

	4
c: y=−		x+13
	3

5) Punkt przecięcia c i d

	4		4
−		x+13=		x−9
	3		3

	8
−		x=−22
	3

	33
x=
	4

y=2 D=(8¹₄,2) ===============

Mariusz: Mila całkiem niezły sposób i może trochę szybszy niż mój Widzę że mój sposób też jest poprawny bo współrzędne szukanego punktu wyszły nam takie same Ja najpierw wyznaczyłem równanie prostej AB a następnie równanie prostej prostopadłej do AB przechodzącej przez środek okręgu Rozwiązując układ równań liniowych dostałem współrzędne punktu styczności Mając współrzędne punktu styczności oraz środka skorzystałem ze wzoru na odległość między dwoma punktami Mając promień wyznaczyłem równania stycznych do okręgu przechodzących przez punkty A oraz C Dostałem dwie pary prostych i wybrałem z nich te proste które nie zawierają odcinków AB oraz BC Z wybranych prostych zapisałem układ równań który dał współrzędne punktu D

Filip: a co jest zlego w kalkulatorze prostym XD Moze od razu dajmy dostep do internetu, laptopa na maturze i niehc korzystaja z dostepnych kalkulatorow w sieci. Dostepny jest kalkulator prosty, poniewaz rachunki na maturze nie wymagaja "wyzszych" kalkulatorow, wiec nie ma sensu ich dawac, po drugie lepiej pisac z niz bez, iz matura z matematyki sa to tylko utarte zadania, schematy, gdzie wystarczy wstawic do wzoru, policzyc na kalkulatorze i tyle

Mariusz: Ja tu w GeoGebrze wyklikałem całe zadanie i wynik wyszedł taki sam jak u Mili a kalkulator prosty to tylko proste obliczenia które ja za czasów maturalnych sprawnie wykonywałem w pamięci bądź pisemnie (Miałem taką nauczycielkę która pokazała mi jak liczyć pisemnie pierwiastek więc wszystkie dostępne na kalkulatorze prostym działania umiałem wykonać pisemnie)

Mila: Gdzie tam szybki, sporo liczenia. Pewnie jest krótszy sposób, ale dziś już nie myślę. Dobranoc

πesio: Korzystam z rys. Mili |AB|=10 . |AS|=5√2, |BS|=5√2 zatem ΔABS jest porostokątny i równoramienny to r=5 i czworokąt ABCD jest trapezem prostokątnym z własności dwusiecznych , kąty przy wierzchołkach A i B są kątami prostymi to: AD ⊥AB i AD ∥ BC

	3		4
aAB=		to aAD= −
	4		3

więc prosta AD ma równanie

	4
AD: y=−		+13
	3

i dalej jak u Mili D(x,y) DC: y=ax+b .............

	4
DC : y=		x−9
	3

to DC∩AD={D}

	4		4		1
		x−9= −		x+13 ⇒ x= 8		i y=2
	3		3		4

D(8¹₄,2) ========

πesio: Poprawiam zapis

	4
AD: y=−		x+13
	3

Mariusz: O i jest szybszy sposób Jak ja chodziłem do szkoły to był w programie jeszcze wzór na równanie prostej przechodzącej przez dwa punkty (Wyglądał tak samo jak wzór na interpolację liniową z użyciem różnic dzielonych Newtona)

Mariusz: https://prnt.sc/12qxke9 Tutaj dokładniejszy rysunek wykonany w GeoGebrze (ukryłem pomocnicze proste i punkt styczności)

πesio: Można jeszcze tak:

	4		4
AD : y= −		x +13 to D=(x, −		x+13)
	3		3

i z tw. Pitagorasa w ΔDSC ( bo |∡DSC|=90^o |DS|²+|SC|²=|DC|² ............................. jak się nie pomylimy w obliczeniach x=8¹₄ i y=2 D=(8¹₄,2) ==========

Filip: γ

πesio: η