pr dzonypieczony: Wyznacz równanie okręgu wpisanego w trójkąt o wierzchołkach A = (−1,3), B = (−5,6), C = (−9,3) pomoze ktos z tym >?

chichi: A gdzie ten środek się znajduje?

dzonypieczony: no punkt przeciecie dwusiecznych

dzonypieczony: ale jak je wyliczyc oto jest pytanie xd

dzonypieczony: dobra cos wyszlo chyba dam rade dokonczyc

Louie314: Na piechotę, ale wcale nie tak długo: Obliczamy pole (gotowy wzór):

	1
P=		|(−5+1)(3−3)−(6−3)(−9+1)|=24
	2

Obliczamy długości boków: |AB|=√(−5+1)²+(6−3)²=√25=5 |BC|=√(−9+5)²+(3−6)²=√25=5 |AC|=√(−9+1)²+(3−3)²=√64=8 Obliczamy połowę obwodu:

	a+b+c		5+5+8
p=		=		=9
	2		2

Obliczamy promień okręgu:

	P		12		4
r=		=		=
	p		9		3

Zauważmy, że trójkąt jest równoramienny, bo |AB|=|BC|. Zatem wysokość opuszczona na bok AC jest dwusieczną kąta CBA, więc środek okręgu leży na prostej prostopadłej do prostej AC. Obliczamy współczynnik kierunkowy prostej AC:

	3−3
aAC=		=0
	−9+1

Zatem prosta AC ma równanie y=3. Zatem prosta prostopadła do tej prostej przechodząca przez punkt B ma równanie x=−5. Stąd na pewno S=(−5,y). Teraz skorzystamy z tego, że środek okręgu musi być odległy od prostej AC o promień okręgu:

	|−y+3|		4
d=		=
	√1		3

	4		4
3−y=		lub 3−y=−
	3		3

	5		13
y=		lub y=
	3		3

Pierwsze rozwiązanie odrzucamy (środek leżałby poza okręgiem). Zatem równanie okręgu to:

	13		16
(x+5)2+(y−		)2=
	3		9

Louie314: Mała poprawka na początku powinno być P=12.

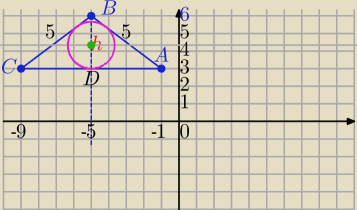
Mila: 1)ΔABC− Δrównoramienny |AC|=8, h=3

	1
PΔ=		*8*3=12
	2

P=(5+5+8}{2}*r 9r=12

	12		4
r=		=
	9		3

	4
2) Srodek okręgu wpisanego w ΔABC leży na dwusiecznej BD w odległości		od AC
	3

D=(−5,3)

	4		1
S=(−5, 3+		)=(−5, 4		)
	3		3

Równanie okręgu:

	13		16
(x+5)2+(y−		)2=
	3		9

piotr: x_s=−5

	|−5*3−4ys+39|
ys−3=		=r
	5

−> y_s=13/3 równanie: (x+5)²+(y−13/3)²=16/9

dzonypieczony: dziekuje bardzo wszystkim