Rownanie 100DniDoMatury:

	1
Wyznacz wszystkie wartości m dla których równanie |1−2x|−|x+3|=−		m2 ma 2 rozne dodatnie
	2

rozwiazania

	1
Na początku myślałem o siatce znaków, ale np. W przedziale (−3,		) dosszedlem do 2x−8=m2
	2

I nie wiedziałem co dalej...

Mila: Próbowałeś metody graficznej?

ICSP: Narysuj wykres funkcji f(x) = |2x − 1| − |x+3| dla x > 0 Następnie zacznij go przecinać prostymi poziomymi y = a i sprawdź dla jakich a takie proste przetną wykres w 2 różnych dodatnich miejscach. P.S. Dlaczego rozważasz równanie dla x < 0 skoro pytają o dodatnie rozwiązania?

100DniDoMatury: Szczerze mówiąc nie pamiętam jak narysować funkcję gdy występuje w niej różnica dwóch wartości bezwzględnych. Mogę prosić o szybkie przypomnienie/wyjaśnienie?

100DniDoMatury: Metoda graficzna była pierwszą o jakiej pomyślałem, ale nie umiałem jej wykonać

ICSP: Rozbij na przypadki:

	1		1
x ∊ (0 ,		] oraz x >
	2		2

Wykres który dostaniesz będzie "sumą" dwóch prostych.

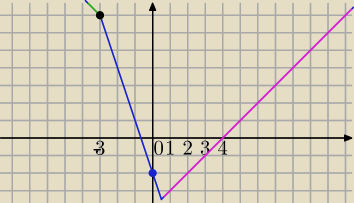
Mila: f(x)= |1−2x|−|x+3|⇔ f(x)=|2x−1|−|x+3|

	1
1) |2x−1|=2x−1 dla x≥
	2

	1
|2x−1|=−2x+1 dla x<
	2

2) |x+3|=x+3 dla x≥−3 |x+3|=−x−3 dla x<−3 =================== 2) x<−3 f(x)=−2x+1−(−x−3)=−2x+1+x+3 f(x)=−x+4 lub

	1
x∊<−3,		)
	2

f(x)=−2x+1−(x+3)=−x−2 f(x)=−x−2 lub

	1
x≥
	2

f(x)=2x−1−x−3 f(x)=x−4 ===========