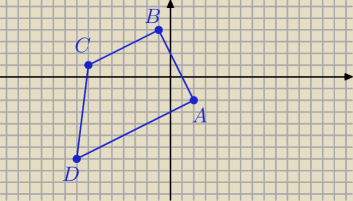
pytanko dzonypieczony: Wykaż, że czworokąt o wierzchołkach w punktach A = (2,−2), B = (−1,4), C = (−7,1) oraz . D = (−8,−7) jest trapezem prostokątnym Czy w takim zadaniu wystarczy, żę wyznacze proste AB oraz AD i że iloczyn ich wspolczynnikow kierunkowych jest rowny −1 ? czy jeszcze coś muszę dopisać żeby był pełen dowód

Tadeusz: dwie proste równoległe i jedna (lub obie) z pozostałych prostopadła do nich

chichi: Trapez to figura mająca przynajmniej jedną parę boków równoległych, a tego nie widać w twoim dowodzie

dzonypieczony: ok dzieki

Tadeusz: oczywiście działasz na samych współczynnikach

janek191: Tak Nie trzeba wyznaczać prostych. Wystarczy wyznaczyć ich współczynniki kierunkowe ze wzoru

	y2 − y1
a =
	x2 − x1

janek191: I oczywiście trzeba sprawdzić,czy pr AD II pr BC

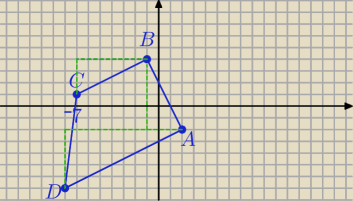
Mila: A = (2,−2), B = (−1,4), C = (−7,1) oraz . D = (−8,−7) jest trapezem prostokątnym 1) Wyznaczamy współrzędne wektorów wektorów: AD^→=[−10,−5], AB^→=[−3,6] [−10,−5] o [−3,6]=−10*(−3)+(−5)*6=0⇔AD⊥AB BC^→=[−6,−3] Sprawdzam, czy BC||AD [−10,−5] [−6,−3]

−10		5
	=
−6		3

−5		5
	=		⇔
−3		3

BC||AD Czworokąt ABCD jest trapezem.