czworokąt mat: Dany jest czworokąt ABCD,w którym |DC|=6, |BC|=5√3, |<BAC|=60⁰,|<ACB|=α Wiedząc,że w czworokąt można wpisać okrąg oraz sinα=0,75 Oblicz długość przekątnej AC i obwód czworokąta

chichi: |AB|=x, |AC|=d

5√3		x		15
	=2R ⇒ 2R=10,		=10 ⇒ x=
√3     2		3     4		2

	15
W czworokąt ABCD można wpisać okrąg → L=2(|AB|+|CD|)=2(6+		)=27
	2

Z tw. Carnota w ΔABC:

	15		15		1		15+5√21
(5√3)2=d2+(		)2−2*		*d*		⇒ d=
	2		2		2		4

P.S. Sprawdź proszę obliczenia

Klara:

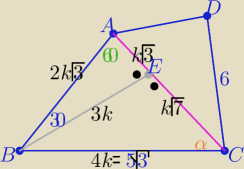
	3
W ΔBCE: sinα=		to.....
	4

W ΔABE "ekierkowym'' o katach ostrych 60^o,30^o .....

	5√3
4k=5√3 ⇒ k=
	4

	15+5√21
|AC|=k(√3+√7) ⇒ |AC|=
	4

|AB|= 7,5 Obwód ABCD : L= 2(7,5+6)= 27

chichi: A więc zgadza się

Klara: