proszę o rozwiązanie anna: dwa boki trójkąta ABC mają długość a i b kąt zawarty między tymi bokami równy α oblicz długość dwusiecznej kąta α zawartego w tym trójkącie jeśli a = 8 b = 6 α = 90⁰

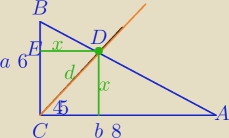
Mila: ΔDEB∼ΔACB

a−x		a
	=		⇔ab−bx=xa ⇔ab=x*(a+b)
x		b

	ab
x=		− długość boku kwadratu
	a+b

	ab√2
d=		− wzór na długość odcinka dwusiecznej kata prostego w Δ prostokatnym
	a+b

o przyprostokątnych a i b.

	6*8√2
d=
	6+8

	24√2
d=
	7

=============

chichi: Można też na siłę z tw. Carnota oraz tw. o dwusiecznej, ale sposób @Mila dużo szybszy

oki:

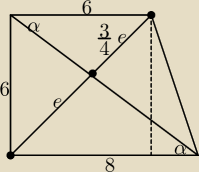
	7		4		24
Szkic;		e = 6√2 /*		, e =		√2
	4		7		7

iko:

chichi:

	a+b+c		2		24√2
s=		=12, d=		√6*8*12*(12−10)=
	2		6+8		7

anna: dziękuję

anna: dwa boki trójkąta ABC mają długość a i b kąt zawarty między tymi bokami równy α oblicz długość dwusiecznej kąta α zawartego w tym trójkącie jeśli a = 8 b = 6 α = 60⁰

	20√3
wynik to
	9

zadanie chciałam wykonać podobnie jak Mila 7maj 21:16 ale nie otrzymałam takiego wyniku tam jest przekątna prostokąta

Mila:

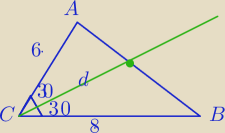
	1
PΔABC=		*8*6*sin60o=12√3
	2

	1		1
12√3=		*d*8sin30o+		*d*6sin30o
	2		2

12√3=2d+1.5d 3.5d=12√3

	12√3		24√3
d=		=
	3.5		7

=================

chichi:

	24√3
No coś nie halo mi ten wynik, ale gubię się ze zmęczenia w obliczeniach, mam d=
	7

chichi: x²=6²+8²−2*6*8*cos(60^o) ⇒ x=2√13

	1		24√3
s=7+√13 ⇒ d=		*√6*8*(7+√13)(7−√13)=
	7		7

Mila: Może inne długości boków?

anna: przepraszam ale rzeczywiście boki to a =4 b = 5 α = 60⁰

chichi: A może za 4 razem okaże się, że to jednak długość środkowej należy wyznaczyć?

chichi: Masz już rozwiązania, teraz sama podstaw swoje dane i wylicz, bo to już będzie szczyt lenistwa..

anna: dziękuję bardzo już rozwiązałam jeszcze raz przepraszam że żle podałam dane

Mila: Nie przejmuj się Czasem tak bywa.

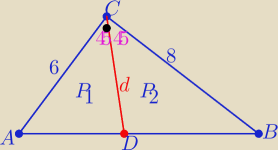
Klara: Zad. z 21:05 można rozwiązać tak: 2P(ABC)=48 i 2P₁=3d√2 i 2P₂=4d√2 to 7d√2=48

	24√2
d=
	7

=========