Zadania z prawdopodobieństwa ze studiów
Damian#UDM:
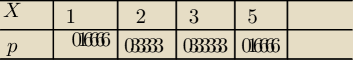
Prawdopodobieństwo studia
1. (0 − 3)
Rzucamy 100 razy symetryczną monetą. Jakie jest prawdopodobieństwo, że
a) orzeł wypadł dokładnie 53 razy,
b) uzyskaliśmy co najmniej 47, ale nie więcej niż 56 orłów.
2. (0 − 3)
Dany jest rozkład zmiennej losowej skokowej X w postaci tabelki:
01666=
16
03333=
13
a) Wyznaczyć analitycznie dystrybuantę i sporządzić jej wykres,
b) Obliczyć wartość oczekiwaną i wariancję zmiennej losowej X.
3. (0 − 5) Zmienna losowa X ma rozkład ciągły, dla którego dystrybuantą jest:
| | ⎧ | 0 dla x<1 | |
| F(x)= | ⎨ | x−1 dla 1≤x≤2 |
|
| | ⎩ | 1 dla x>2 | |
a) Sporządzić wykres dystrybuanty. Wyznaczyć gęstość i sporządzić jej wykres.
b) Obliczyć wartość oczekiwaną i wariancję zmiennej losowej X.
4. (0 − 3) Wzrost mieszkańców Liliputlandii jest zmienną losową posiadającą rozkład normalny
o parametrach
μ=40 i σ=10 [w cm].
a) Obliczyć jaką część mieszkańców ma wzrost mieszczący się w przedziale od 35 do 42 cm.
b) Wybrano losowo 25 mieszkańców. Jakie jest prawdopodobieństwo, że w sumie mają więcej niż 960
cm?
Proszę o pomoc, wskazówki i rozwiązania, chciałbym to ogarnąć

6 maj 11:51
getin:
Zad. 1
b)
Ω = 2
100
6 maj 12:05
6 maj 13:54
Damian#UDM: 1. (0 − 5)
Zmienna losowa ma rozkład ciągły, dla którego funkcją gęstości jest:
| | ⎧ | 18x dla x∊<0,4> | |
| f(x)= | ⎩ | 0 dla pozostałych. |
|
a) Sporządzić wykres gęstości. Wyznaczyć dystrybuantę i sporządzić jej wykres.
b) Obliczyć wartość oczekiwaną i wariancję.
2. (0 − 4)
Wzrost mieszkańców Liliputlandii jest zmienną losową posiadającą rozkład normalny o
parametrach μ=40 i σ=10 [w cm]. Obliczyć,
a) jaka część mieszkańców ma wzrost większy niż 45 cm,
b) jaka część mieszkańców ma wzrost mieszczący się w przedziale od 35 do 42 cm.
Proszę o pomoc, rozwiązania

10 maj 13:20
Mila:
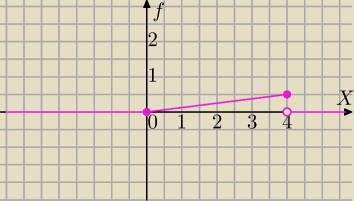
1)
Wykres gęstości:
2) Dystrybuanta:
a)x<0
F(x)=
−∞∫
xf(t)dt=
−∞∫
0 0dt=0
b) x∊<0,4>
| | 1 | |
F(x)=−∞∫xf(t)dt=−∞∫0 0dt+0∫x |
| t dt+4∫∞0dt= |
| | 8 | |
| | 1 | | 1 | |
=[ |
| t2]0x= |
| x2 ( wynikiem ma być funkcja) |
| | 16 | | 16 | |
c)x>4
Uwzględniamy wszystkie przedziały ( skumulowane szanse)
| | 1 | |
F(x)=−∞∫xf(t)dt=−∞∫0 0dt+0∫4 |
| t dt+4∫∞0dt= |
| | 8 | |
| | 1 | | 1 | |
=[ |
| 2]04= |
| *42−0=1 |
| | 16t | | 16 | |
wykres w następnym wpisie.
10 maj 20:30
Mila:
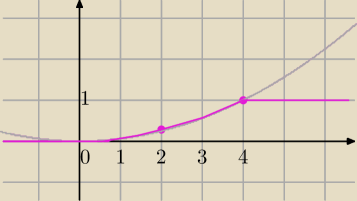
Różowy wykres.
3) Wartość oczekiwana:
| | 1 | |
E(X)=−∞∫∞x*f(x) dx=0+0∫4 |
| x2 dx+0= |
| | 8 | |
4) Wariancja :
D
2(X)=E(X
2)−(E(X))
2
| | 1 | | x3 | | x4 | |
E(X2)=0∫4(x2* |
| x) dx=0∫4 |
| dx=[ |
| ]04= |
| | 8 | | 8 | | 32 | |
| | 8 | | 64 | | 8 | |
D(X)=8−( |
| )2=8− |
| = |
| |
| | 3 | | 9 | | 9 | |
10 maj 20:49
10 maj 21:03
Mila:
I co, policzyłeś?
10 maj 23:34
Mila:
Rozkład normalny o
parametrach μ=40 i σ=10 [w cm]. Obliczyć,
a) jaka część mieszkańców ma wzrost większy niż 45 cm,
b) jaka część mieszkańców ma wzrost mieszczący się w przedziale od 35 do 42 cm.
X− wzrost mieszkańca L...
Standaryzujemy zmienną X, wartości dystrybuanty odczytujemy z tablic.
| | X−40 | | 45−40 | |
P(X>45)=P( |
| > |
| )=P(Z>0.5)= |
| | 10 | | 10 | |
=1−P(Z<0.5)= odczytujesz z tablic
=1−0.6915=0.3085
około 0.3 całej populacji ma wzrost większy niż 45 cm
b)
35<X<42
| | 35−40 | | X−40 | | 42−40 | |
P(35<X<42)=P( |
| < |
| < |
| )= |
| | 10 | | 10 | | 10 | |
=P(−0.5<Z<0.2)=P(Z<0.2)−P(Z<−0.5)=
=P(Z<0.2)−P(Z>0.5)=
=P(Z<0.2)−(1−P(Z<0.5))=..
dokończ
11 maj 23:17
figa:
Nie ma odzewu od wczoraj ...

11 maj 23:25
Mila:
20:49 ostatnia linijka powinna być taka:
12 maj 17:06
ite:
Damian#UDM miał poprawiać maturę rozszerzoną, więc pewnie chce trochę odetchnąć.
12 maj 21:12
Mila:
Dobry wieczór
ite. Skoro jesteś, to może sprawdzisz moje rozwiązanie?
Trochę mi ta wiedza zardzewiała, nie chciałabym zamącić w głowie Damianowi

12 maj 21:43
Damian#UDM: Hej! Bardzo dziękuję
Milu za rozwiązania oraz reszcie za odzew !

Na szczęście to zadanie z dystrybuantą oraz gęstością udało mi się rozwiązać z filmikiem z
youtube, dziękuję bardzo za okazaną mi pomoc

Tak, poprawiałem maturę i niestety nie poprawiłem

Będzie wynik w przedziale 88 − 92 % .
Poległem na zadaniu z dowodem geometrycznym, zrobiłem błąd w rachunkach i dalej już nic nie
mogłem znaleźć. W 14. (0 − 6) nie wyznaczyłem dokładnego przedziału dla trójkąta ostrokątnego,
rozpatrzyłem tylko warunek a
2 + b
2 > c
2 oraz w 15. (0 − 7) na pewno znów poleci mi punkt za
dziedzinę, ponieważ zapisałem tylko, że a∊(0,9) oraz c∊(0,9), gdzie a − długości krawędzi
podstawy prostopadłościanu oraz c − wysokość prostopadłościanu.
No i najgorsze, w zadaniu 2. (0 − 1) zaznaczyłem złą odpowiedź. Niestety.
Arkusz możecie znaleźć pod linkiem:
https://static2.cke.gov.pl/images/_EGZAMIN_MATURALNY_OD_2015/Arkusze_egzaminacyjne/2021/Matematyka/poziom_rozszerzony/EMAP-R0-100-2105.pdf
14 maj 22:20
Damian#UDM: Mila wszystkie wartości oraz wykresy w tym zadaniu wyszły mi takie same

dziękuje za
zapisanie tutaj rozwiązań

14 maj 22:21
chichi:
Przy 9 i tak powinno być domknięcie, więc nawet jakbyś ograniczył od 4 do 9, to punktu by nie
było

14 maj 22:23
Damian#UDM: Wiem o tym

14 maj 22:30
Damian#UDM: Szkoda, że dopiero po maturze

14 maj 22:30
Mila:

14 maj 22:54
Damian#UDM: zadanie 7.
Zmienna losowa X ma rozkład ciągły, dla którego dystrybuantą jest:
| | ⎧ | 0 dla x<0 | |
| f(x)= | ⎨ | 19x2 dla 0≤x≤3 |
|
| | ⎩ | 1 dla x>3 | |
a) Sporządzić wykres dystrybuanty. Wyznaczyć gęstość i sporządzić jej wykres.
b) Obliczyć wartość oczekiwaną i wariancję zmiennej losowej X.
A jak postąpić w takim przypadku? Liczyć pochodne każdej funkcji na każdym przedziale i
wystarczy? Czy jednak szukać najmniejszej wartości w podanym przedziale za pomocą pochodnej?
Proszę o pomoc

20 maj 12:28
ICSP: Po co chcesz szukać najmniejszej wartości?
20 maj 12:32
Damian#UDM: No bo jak mam funkcję gęstości to wtedy, żeby obliczyć dystrybuantę to liczę całkę ∫
x−∞,
oczywiście dalej w zależności jakie mam przedział i dlatego myślałem, że w drugą stronę będzie
podobnie.
Proszę po prostu o rozjaśnienie jak to się poprawnie powinno robić i wszystko będzie ok

20 maj 14:05
ICSP: Masz podaną dystrybuantę i chcesz wyznaczyć funkcję gęstości. (nie na odwrót)
Rozkład jest ciągły, więc możesz to zrobić.
Różniczkujesz dystrybuantę przedziałami i w ten sposób otrzymasz funkcję gęstości.
Tutaj nie ma nic związanego z szukaniem najmniejszej wartości w podanym przedziale.
Dlatego powtórzę pytanie:
Dlaczego chcesz szukać najmniejszej wartości? Co ci to da?
20 maj 14:11
Damian#UDM: Po prostu szukam schematu na to zadanie i rzuciłem luźny pomysł podobny do liczenia
dystrybuanty gdy mam podaną gęstość

20 maj 22:07
Damian#UDM: zadanie 7.
| | ⎧ | 0 dla x<0 | |
| f(x)= | ⎨ | 19x2 dla 0≤x3 |
|
| | ⎩ | 1 dla x>3 | |
1. dla x<0
f(x)=0
f'(x)=0
2. dla 0≤x≤3
f(x)=
19x
2
f'(x)=
29x
3. dla x>3
f(x)=1
f'(x)=0
Funkcja funkcja gęstości
| | ⎧ | 0 dla x<0 | |
| F(x)= | ⎨ | 29x dla 0≤x3 |
|
| | ⎩ | 0 dla x>3 | |
Jest ok ?
20 maj 22:15
ICSP: Masz podaną
dystrybuantę (oznaczyłeś ją małą literą f jak to w zwyczaju oznacza się
gęstość − to może być powodem twojego zmieszania) i masz obliczyć gęstość (12:28 − pierwsza
linijka)
Następnie chcesz obliczyć dystrybuantę mając funkcję gęstości (14:05 , 22:07)
Mam wrażenie, że trochę się pogubiłeś w tym co masz zrobić.
Masz daną dystrybuantę:
| | ⎧ | 0 dla x < 0 | |
| F(x) = | ⎨ | x2/9 dla 0 ≤ x ≤ 3 |
|
| | ⎩ | 1 dla x > 3 | |
ponieważ jest ona ciągła to aby wyznaczyć gęstość różniczkujesz ją przedziałami (akurat w tym
przykładzie będzie różniczkowalna, wiec możesz tak zrobić).
20 maj 22:20
ICSP: Obliczenia poprawne
Oznaczenia nie.
F(x) − dystrybuanta
f(x) − funkcja gęstości
20 maj 22:23
Damian#UDM: To prawda, pomyliłem te znaki. Dziękuje za pomoc

20 maj 22:23
Mila:
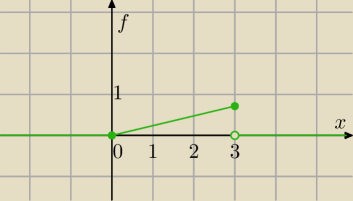
1) Dystrybuanta : wykres narysuj sam
(0 dla x<0
(1 dla x>3
2) f(x)− funkcja gęstości
(0 dla x<0
( 0 dla x>3 (na rysunku)
3)Wartość oczekiwana:
| | 2 | |
E(X)=−∞∫∞(x*f(x)) dx=0+0∫3( |
| x2) dx+0= |
| | 9 | |
4) Wariancja
D
2(X)=E(X
2)−(E(X))
2
| | 2 | | 2 | |
E(X2)=−∞∫∞(x2*f(x)) dx=0∫3( |
| x3) dx=[ |
| x4]03= ... licz dalej sam |
| | 9 | | 36 | |
20 maj 22:31
Damian#UDM: A wariancję i wartość oczekiwaną nadal liczę z dystrybuanty?
20 maj 22:32
Damian#UDM: czyli liczę z gęstości, Dziękuję

20 maj 22:33
Damian#UDM: No musiałem się po prostu pomylić. Dziękuję wam.
20 maj 22:51
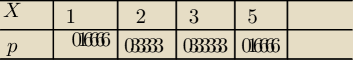 Prawdopodobieństwo studia
1. (0 − 3)
Rzucamy 100 razy symetryczną monetą. Jakie jest prawdopodobieństwo, że
a) orzeł wypadł dokładnie 53 razy,
b) uzyskaliśmy co najmniej 47, ale nie więcej niż 56 orłów.
2. (0 − 3)
Dany jest rozkład zmiennej losowej skokowej X w postaci tabelki:
01666=16
03333=13
a) Wyznaczyć analitycznie dystrybuantę i sporządzić jej wykres,
b) Obliczyć wartość oczekiwaną i wariancję zmiennej losowej X.
3. (0 − 5) Zmienna losowa X ma rozkład ciągły, dla którego dystrybuantą jest:
Prawdopodobieństwo studia
1. (0 − 3)
Rzucamy 100 razy symetryczną monetą. Jakie jest prawdopodobieństwo, że
a) orzeł wypadł dokładnie 53 razy,
b) uzyskaliśmy co najmniej 47, ale nie więcej niż 56 orłów.
2. (0 − 3)
Dany jest rozkład zmiennej losowej skokowej X w postaci tabelki:
01666=16
03333=13
a) Wyznaczyć analitycznie dystrybuantę i sporządzić jej wykres,
b) Obliczyć wartość oczekiwaną i wariancję zmiennej losowej X.
3. (0 − 5) Zmienna losowa X ma rozkład ciągły, dla którego dystrybuantą jest:


 1)
Wykres gęstości:
2) Dystrybuanta:
a)x<0
F(x)=−∞∫xf(t)dt=−∞∫0 0dt=0
b) x∊<0,4>
1)
Wykres gęstości:
2) Dystrybuanta:
a)x<0
F(x)=−∞∫xf(t)dt=−∞∫0 0dt=0
b) x∊<0,4>
 Różowy wykres.
3) Wartość oczekiwana:
Różowy wykres.
3) Wartość oczekiwana:


 Na szczęście to zadanie z dystrybuantą oraz gęstością udało mi się rozwiązać z filmikiem z
youtube, dziękuję bardzo za okazaną mi pomoc
Na szczęście to zadanie z dystrybuantą oraz gęstością udało mi się rozwiązać z filmikiem z
youtube, dziękuję bardzo za okazaną mi pomoc  Tak, poprawiałem maturę i niestety nie poprawiłem
Tak, poprawiałem maturę i niestety nie poprawiłem Będzie wynik w przedziale 88 − 92 % .
Poległem na zadaniu z dowodem geometrycznym, zrobiłem błąd w rachunkach i dalej już nic nie
mogłem znaleźć. W 14. (0 − 6) nie wyznaczyłem dokładnego przedziału dla trójkąta ostrokątnego,
rozpatrzyłem tylko warunek a2 + b2 > c2 oraz w 15. (0 − 7) na pewno znów poleci mi punkt za
dziedzinę, ponieważ zapisałem tylko, że a∊(0,9) oraz c∊(0,9), gdzie a − długości krawędzi
podstawy prostopadłościanu oraz c − wysokość prostopadłościanu.
No i najgorsze, w zadaniu 2. (0 − 1) zaznaczyłem złą odpowiedź. Niestety.
Arkusz możecie znaleźć pod linkiem:
https://static2.cke.gov.pl/images/_EGZAMIN_MATURALNY_OD_2015/Arkusze_egzaminacyjne/2021/Matematyka/poziom_rozszerzony/EMAP-R0-100-2105.pdf
Będzie wynik w przedziale 88 − 92 % .
Poległem na zadaniu z dowodem geometrycznym, zrobiłem błąd w rachunkach i dalej już nic nie
mogłem znaleźć. W 14. (0 − 6) nie wyznaczyłem dokładnego przedziału dla trójkąta ostrokątnego,
rozpatrzyłem tylko warunek a2 + b2 > c2 oraz w 15. (0 − 7) na pewno znów poleci mi punkt za
dziedzinę, ponieważ zapisałem tylko, że a∊(0,9) oraz c∊(0,9), gdzie a − długości krawędzi
podstawy prostopadłościanu oraz c − wysokość prostopadłościanu.
No i najgorsze, w zadaniu 2. (0 − 1) zaznaczyłem złą odpowiedź. Niestety.
Arkusz możecie znaleźć pod linkiem:
https://static2.cke.gov.pl/images/_EGZAMIN_MATURALNY_OD_2015/Arkusze_egzaminacyjne/2021/Matematyka/poziom_rozszerzony/EMAP-R0-100-2105.pdf
 dziękuje za
zapisanie tutaj rozwiązań
dziękuje za
zapisanie tutaj rozwiązań 








 1) Dystrybuanta : wykres narysuj sam
(0 dla x<0
1) Dystrybuanta : wykres narysuj sam
(0 dla x<0
