podprzestrzeń liniowa salamandra: Sprawdź, czy podany zbiór jest podprzestrzenią danej przestrzeni liniowej:{(x, y)∈R²: xy≥0} w R² Czy wystarczy podać przykład, np. w₁= (−2,−2) α=−1 w₂ = (−1,−4) β=1 wtedy v=αw₁+βw₂ = (2,2)+(−1,−4) = (1,−2), więc x*y < 0? więc nie jest to podprzestrzeń liniowa?

ite: jak określona jest przestrzeń liniowa i jaki zbiór ma być jej podprzestrzenią?

salamandra: Wysłałem całą treść zadania

ite: na końcu jest R², nie doczytałam czyli przestrzeń tworzą pary liczb rzeczywistych, a sprawdzamy czy podprzestrzenią będą pary liczb, których iloczyn jest nieujemny

salamandra: Czyli moje uzasadnienie jest ok?

Adamm: Jeśli przestrzeń liniowa w Rⁿ ma niepuste wnętrze, to jest całym Rⁿ Faktycznie, jeśli kula o środku x i promieniu r zaiwera się w p. l. M to również kula o środku w 0 i promieniu r. Stąd, wektor av jest w M dla odpowiednio małego a>0 i dowolnego v. Zatem i v jest w M, czyli M = Rⁿ

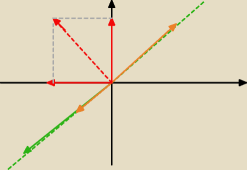
ite: Taki prostszy wariant odpowiedzi: 1/ skalowanie wektorów o współrzędnych (x,y) spełniających warunek z 11:39 tworzy wektory, których współrzędne nadal spełniają warunek x*y≥0, 2/ ale dodawanie takich wektorów już nie v = v₁+v₂ = (−5,0)+(0,5) = (−5,5) −5*5<0 więc nie jest to podprzestrzeń v=αv₁+βv₂, współczynniki α i β są przydatne jeśli masz konkretny wektor v i musisz go przedstawić jako sumę dwóch innych o podanych wspórzędnych, przy wskazaniu kontrprzykładu nie są potrzebne

salamandra: Hm, dziwne, bo wykładowca mi powiedział, że moje uzasadnienie jest złe, ponieważ "wektor v nie ma takiej postaci" i nie zaliczył mi zadania.

ite: może komuś będzie się chciało spojrzeć na to, co napisałam i poprawi

jc: Salamandra, w porządku, choć można było krócej. Wektory (−3, −1), (2, 2) należą do rozpatrywanego podzbioru R², ale ich suma (−3, −1) + (2, 2) = (−1, 1) nie należy. Dlatego zbiór nie jest podprzestrzenią R².

salamandra: Dlaczego w takim razie mój wykładowca twierdzi, że wektor v nie ma takiej postaci?

mateusz: twoje rozwiązanie jest poprawne. tutaj na stronie 5 jest uzasadnienie http://prac.im.pwr.edu.pl/~jakubow/algebra_liniowa_1/wyklad7.pdf

Adamm: Alternatywnie Można udowodnić, że jeśli H ma dodatnią miarę Lebesgue'a, to H = Rⁿ. W szczególności, jeśli H zawiera kulę otwartą, to H ma dodatnią miarę Lebesgue'a, więc H = Rⁿ.