pr
dzonypieczony: W kwadracie ABCD o boku długości 12 punkt E jest środkiem boku AB , punkt F jest
środkiem boku AD . Punkt G dzieli bok AB w stosunku 1:2 licząc od wierzchołka A ,
natomiast punkt H dzieli bok BC w stosunku 2:1 licząc od wierzchołka B . Odcinki EF i
GH przecinają się w punkcie J . Oblicz długość odcinka CJ
pomoze ktos ?
4 maj 22:09
Mila:
Dwa razy masz podział boku AB. Tak ma być?
4 maj 22:18
dzonypieczony: tak
4 maj 22:47
janek191:
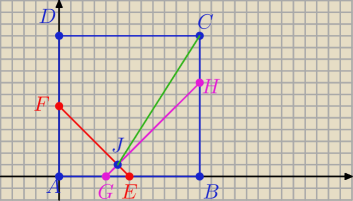
pr. EF
y = − x + 6
pr. GH
y = x − 4
więc
− x + 6 = x − 4
2 x = 10
x = 5
y = 5 − 4 = 1
J = ( 5, 1)
========
C = ( 12, 12) J = ( 5,1)
I C J I
2 = (5 − 12)
2 = ( 1 − 12)
2 = (−7)
2 + ( −11)
2 = 49 + 121 = 170
zatem
I CJ I =
√170
==============
5 maj 07:14
Mila:
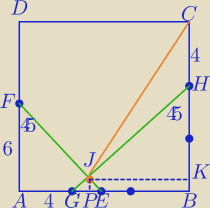
ΔGEJ− Δprostokątny o przeciwprostokątnej równej 2
|PJ|=|BK|=1
|JK|=7
|JC|
2=11
2+7
2
|JC|=
√170
5 maj 16:23
chichi:
No ładnie go nazwałaś @
Mila 
5 maj 17:20
Mila:
Tak jak autor chciał

Bardzo nowocześnie.
5 maj 17:43
 pr. EF
y = − x + 6
pr. GH
y = x − 4
więc
− x + 6 = x − 4
2 x = 10
x = 5
y = 5 − 4 = 1
J = ( 5, 1)
========
C = ( 12, 12) J = ( 5,1)
I C J I2 = (5 − 12)2 = ( 1 − 12)2 = (−7)2 + ( −11)2 = 49 + 121 = 170
zatem
I CJ I = √170
==============
pr. EF
y = − x + 6
pr. GH
y = x − 4
więc
− x + 6 = x − 4
2 x = 10
x = 5
y = 5 − 4 = 1
J = ( 5, 1)
========
C = ( 12, 12) J = ( 5,1)
I C J I2 = (5 − 12)2 = ( 1 − 12)2 = (−7)2 + ( −11)2 = 49 + 121 = 170
zatem
I CJ I = √170
==============
 ΔGEJ− Δprostokątny o przeciwprostokątnej równej 2
|PJ|=|BK|=1
|JK|=7
|JC|2=112+72
|JC|=√170
ΔGEJ− Δprostokątny o przeciwprostokątnej równej 2
|PJ|=|BK|=1
|JK|=7
|JC|2=112+72
|JC|=√170

 Bardzo nowocześnie.
Bardzo nowocześnie.