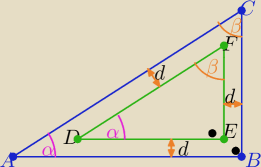
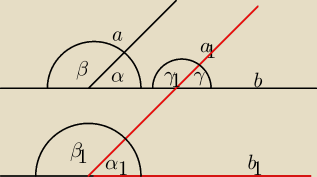
Dowód Czas kosić trawniki: Kąty o ramionach odpowiednio równoległych Rysunek przedstawia pare takich kątów α i α₁ których odpowiednie ramiona są parami równoległe tzn aIIa₁ i bIIb₁ Chcemy udowodnić twierdzenie że kąty αi α₁ są rowne To twierdzenie udowodnimy z zastrzeżeniem że oba nasze kąty są albo ostre tak jak α i α₁ albo rozwarte tak jak β i β₁ Twierdzenie Jeśli dwa kąty mająramiona odpoweidnie do siebie równoległe to kąty te są równe (jeśli oba są ostre lub rozwarte) Założenie : aIIa₁ i bIIb₁ Teza : Kąt α= Kątowi α₁ Dowód : Posłużmy sie pomocniczym kątem γ który powstał przez przecięcie się nierównoległych ramion a₁ i b Tworzy on wraz z kątem α parę kątow odpowiadających Kąt α= Kątowi γ Ten sam kąt γ tworzy z kątem α₁ również parę kątow odpowiadających (równoległe b i b₁ przeciete sieczna a₁) Kąt α₁=Kątowi γ Z otrzymanych równości wynika że kąt α=kątowi α₁ c.k.d Przeprowadzić taki sam dowód w odniesieniu do pary kątów rozwartych β i β₁ posługując się w tym przypadku kątem pomocniczym γ₁

och&ach: Chcesz się nauczyć geometrii? To jak długo będziesz "bawić się klockami" ? Może lepiej już idź "kosić te trawniki"

Czas kosić trawniki: Wykażcie , że trójkąt utworzony przez zewnętrzne krawędzie krawędzie ekierki oraz trójkat którego bokami sa krawędzie wewnętrzne mają kąty odpowiednio równe

och&ach:

och&ach: Jeżeli ramiona dwóch kątów są równoległe, to.......................

Czas kosić trawniki: Dziękuje . Wlaśnie z rana szykowałem kosiarkę do akcji