podprzestrzenie salamandra: Zbadać, które z podanych zbiorów wektorów są podprzestrzeniami odpowiedniej przestrzeni wektorowej (a) wektory płaszczyzny o początku w punkcie O = (0, 0), których końce leżą na jednej z dwóch różnych prostych przecinających się w punkcie O; (b) wektory płaszczyzny o początku w punkcie O, których końce leżą na danej prostej; Czy ktoś mógłby podpowiedzieć, jak się robi takie zadania?

salamandra: mam takie rozwiązanie, ale nie rozumiem co tu się dzieje: a) v₁, v₂ ∊ W v₁= (x₁,y₁) v₂=(x₂,y₂) v = α*v₁ + β*v₂ v= (α*x₁+β*x₂, α*y₁+β*y₂) v=(x,y) ∊ W Jest podprzestrzenią. Nie rozumiem skąd ten wniosek, że jest tą podprzestrzenią?

salamandra: b) v₁= (x₁,y₁) v₂= (ax₁, ay₁) α,β,a,b ∊ R v=α*v₁+β*v₂ v=(α*x₁,α*y₁)+(βax₁,βay₁) v=((α+βa)x₁, (α+βa)y₁) α+βa = b v=(bx₁,by₁) Jest podprzestrzenią. tutaj również nie rozumiem skąd stwierdzenie, że jest to podprzestrzeń I skąd w ogóle wartości dla v₂, że jest to (ax₁, ay₁). Proszę o jakąkolwiek wskazówkę. W sieci znajduję tylko przykłady na konkretnych zbiorach, ale takiego konkretnego zadania nigdzie nie znalazłem i nie mam na czym się wzorować, oprócz tej odpowiedzi, którą podałem.

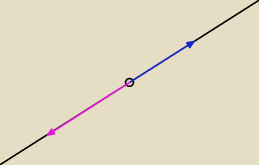
ite: (b) wektory płaszczyzny o początku w punkcie O, których końce leżą na danej prostej; więc można spojrzeć na wektor v₂ jako na "przeskalowanie" tego pierwszego wektora

salamandra: No to w sumie jest jasne, jednak nie bardzo wiem, na czym polega ten dowod, znaczy− znam warunki, ale nie wiem, dlaczego w tych przypadkach one zachodzą? Na jakiej podstawie?

ite: Pokazałeś, że suma dwóch dowolnych wektorów, których końce leżą na danej prostej, też będzie wektorem, którego koniec leży na tej samej prostej. v=((α+βa)x₁, (α+βa)y₁)

salamandra: Prawdę mówiąc, to spisałem odpowiedź i nie wiem, skąd wniosek, że koniec tego wektora będzie również na tej prostej?

ite: obie współrzędne wektora v powstały z pomnożenia współrzędnych wektora v₁ (z założenia leżącego na tej prostej) przez jednakowe współczynniki liczbowe (α+βa)

salamandra: No tak, przecież.... A co jeśli chodzi o a)?

ite: w pierwszym mam wątpliwość, nie wiem, 1/ czy bierzemy pod uwagę wektory o końcach tylko na jednej z dwóch różnych prostych przecinających się w punkcie O (z dwóch prostych wybieramy tylko jedną i mamy sytuację tak jak w b/), 2/ czy końce wektorów leżą na obu prostych (i koniec wektora będącego ich sumą nie musi leżeć na żadnej z nich) może wypowie się ekspert?

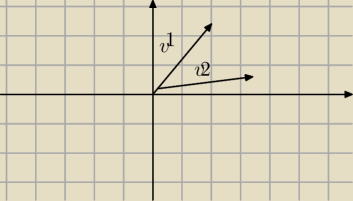
salamandra: Mam pomocniczy rysunek do a), jeśli to coś pomoże:

ite: czyli końce wektorów mogą leżeć na dwóch różnych prostych, koniec wektora będącego ich sumą nie leży na żadnej z tych prostych nie zgadza mi się wniosek w podanej odpowiedzi, niech ktoś mnie poprawi, jeśli się mylę

salamandra: A jeżeli byłaby ta druga opcja, to jakie byłoby uzasadnienie?

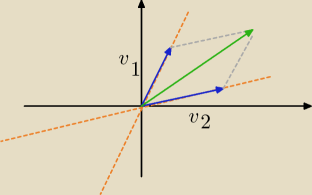
ite: koniec wektora będącego sumą tych dwóch narysowanych nie leży na żadnej z zadanych prostych, a więc nie należy do W czyli pierwszy warunek konieczny do tego, żeby ten zbiorów wektorów był podprzestrzenią nie jest spełniony (jeśli prawidłowo odczytałam warunki z 18:25)

Maciess: a) odpada

salamandra: dzięki, kompletnie nie wiedziałem, skąd ten wniosek w a), a tym bardziej skąd nagła zamiana na (x,y) i stwierdzenie, że jest podprzestrzenią