Punkt A (15, -5) jest wierzchołkiem trójkąta prostokątnego o kącie prostym przy kosek: Punkt A (15, −5) jest wierzchołkiem trójkąta prostokątnego o kącie prostym przy wierzchołku B, opisanego na okręgu x² + y² = 25. Wyznacz wierzchołki B i C tego trójkąta, wiedząc, że jego przeciwprostokątna jest równoległa do osi OX. Bardzo proszę o wyjaśnienie

Legend of Fuyao: Zrozumiesz jak zrobisz rysunek do zadania

kosek: zrobilem rysunek i nie idzie mi, wytlumaczenie w ksiazce jest strasznie dziwne i nieklarowne, dlatego prosze o pomoc

Filip:

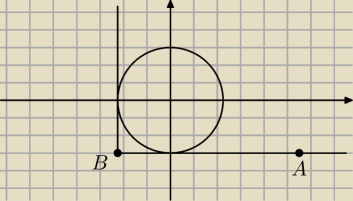
Filip: można odczytać, że punkt B ma wspólrzedne (−5, −5)

kosek: wedlug ksiazki B = (−1,7)

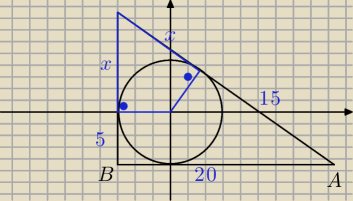
Filip: co wiecej, zauwaz ze punkt C ma wspolrzedne (−5, x), teraz z pitagorasa: (x + 5)² + 20² = (15 + x)² liczysz x

Filip: przepraszam najmocniej, nie zauwazylem ze PRZECIWPROSTOKATNA ma byc rownolegla do osi x

Louie314: Najpierw rysujesz styczną do okręgu równoległą do osi OX, która przechodzi przez punkt A(15,−5). Łatwo wyznaczysz jej równanie (w tej prostej zawierać się będzie przeciwprostokątna). Następnie wyznaczasz drugą styczną do okręgu, która przechodzi przez punkt A(15,−5) (skorzystaj z tego, że jest to prosta przechodząca przez punkt A, a jej odległość od środka okręgu wynosi 5). Potem znajdujesz styczną do okręgu, która jest prostopadła do wyznaczonej właśnie stycznej (znowu skorzystaj z odległości tej prostej od środka okręgu). Gdy wyznaczysz już wszystkie te styczne, to wystarczy, że policzysz punkty ich przecięć − to będą wierzchołki trójkąta. Powinno wyjść: B=(−1,7) C=(−10,−5)

kosek: przy ostatniej stycznej BC wychodzą mi dwa rozne b, nie wiem ktory odrzucic

kosek: a dobra, ten ujemny nie moze byc bo przecinałby oś OY w punkcie ujemnym a to nie pasuje

kosek: dziekuje za pomoc, wyszło pozdrawiam

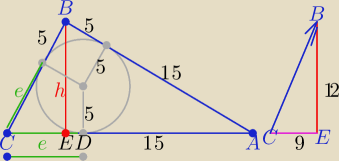
πesio: Podaję taki sposób ( może ktoś skorzysta) z tw. o odcinkach stycznych ( dane na rys. z tw. Pitagorasa : (e+15)²=(e+5)²+20²⇒ ... e=|CD|=10 |CD|=10 i D=(0,−5) i C(x, −5) to C(−10,−5)

	15*20
to |AB|=20, |AC|=25, |BC|=15 to h=		=12
	25

|CE|= √15²−12²= 9 to → CB= [9,12] więc B=(−10+9, −5+12) =(−1,7) odp: C(−10,−5) , B(−1,7) =================