Dwa okręgi
Legend of Fuyao:
zadanie
Udowodnić że gdy dwa okręgi przecinają się w punktach P i Q wtedy linia środków O1O2 jest
symetralną odcinka PQ
2 maj 20:54
Legend of Fuyao:
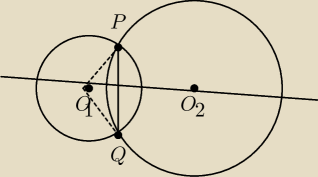
Gdyby udało się udowodnic że trójkąt Q O
1P jest równoranienny to byloby po zadaniu
2 maj 21:33
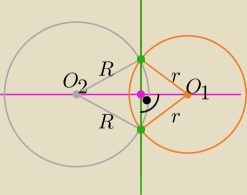
Filip: oczywiscie ze jest Q1Q = Q1P = rmniejszego okregu wizualnie
2 maj 21:34
πesio:
2 maj 22:00
Legend of Fuyao: O mój Jezu .
dlaczego ja nie pomyslaem że sa to promienie okręgow ? Zacmienie jakies czy cus
Więc tak oba trojkąty rownoramienne o wspolnej podstawie PQ
Z wlasnosci trojkata rownoramiennego wysokosc dzieli podstawe na polowy i pada na nią pod kątem
prostym
A mozna z tego skorzystac ze w trojkącie rownoramiennym srodkowa wzgledem podstawy ,
dwusieczna kąta zawartego miedzy ramionami i wysokosc wzgledem podstawy pokrywaja sie
Wobec tego srednica okregu prostopadle do cieciwy dzieli ja na polowy
2 maj 22:40
πesio:

2 maj 22:44
Filip:

2 maj 23:45
 Gdyby udało się udowodnic że trójkąt Q O1P jest równoranienny to byloby po zadaniu
Gdyby udało się udowodnic że trójkąt Q O1P jest równoranienny to byloby po zadaniu


