pr dzonypieczony: Stosunek pola trójkąta równobocznego opisanego na okręgu do pola trójkąta równobocznego wpisanego w ten okrąg wynosi: pomocy

Legend of Fuyao: Dobrze jest pamiętać że w trójkącie rownobocznym bok a jest równy a=√3R R−promien okręgu opisanego na trójkącie lub a=2√3r r− promień okręgu wpisanego w trójkąt więc S− pole

	1		3
S=		√3a2=		√3R2=3√3r2
	4		4

πesio: 4

πesio: No i po ptokach

silnia: Wytlumaczy ktos, bo nie rozumiem...

Mila: Umiesz coś o Δ równobocznym?

silnia: Tak, po prostu glowa mi szwankuje akurat przy tym

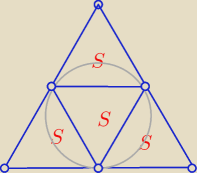
Eta: Pdużego Δ=4S PmałegoΔ=S

4S
	=4
S

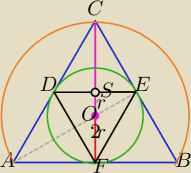
Mila: Różne są sposoby: 1) Δ są podobne h=|SF|=2r+r=3r−wysokość ΔDEF 2) H=|FC|=2r+|OC|=2r+4r =6r −wysokość ΔABC

|FC|		6r
	=		=2=k skala podobieństwa Δ
|FS|		3r

Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa

	PΔABC
k2=		=22=4
	PΔDEF

2) To zadanie to pewnie test wyboru, możesz przyjąć, że np.2r=4, to r=2 wtedy h=6, H=12

	H
i dalej		=2
	h

k²=4