Na czworokącie wypukłym ABCD można opisać okrąg. Marysia: Na czworokącie wypukłym ABCD można opisać okrąg. Wiadomo, że IABI = IBCI, IADI = 2√3, IDCI = 3 − √3 oraz przekątna IACI = 3√2. Oblicz pole tego czworokąta.

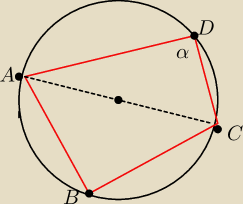
Legend of whitesnake : W trójkącie ADC z tw cosinusow oblicz kąt α W warunku opisania na czworokącie okregu wylicz kąt ABC= 180^o−α Trójkąt ABC jest rownoramienny wiec zastanow sie jak obliczyc dlugosc boku AB czy BC Pole czworokata ABCD = pole ΔADC+pole ΔABC

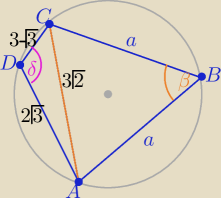
πesio: 1/ z tw. cosinusów w ΔADC

	(2√3)2+(3−√3)2−(3√2)2		1
cosδ=		=...... = −
	2*2√3*(3−√3)		2

zatem δ= 120^o to β= 60^o ( sama odpowiedz dlaczego?) więc ΔABC jest równoboczny o boku a= 3√2 P(ABCD)= P(ΔADC) +P(ΔABC)=.......... teraz sama dokończ obliczenia

πesio: @ "Legendy..." |AC|≠ 2R W zadaniach nie należy wprowadzać mylnego rysunku !

Legend of whitesnake : Proszę napisać co jest błedne ? narysowałem zgodnie z treścia AB=BC i AD>CD Na początku zadania nie wiem ze ΔABC jest rownoboczny to wiem tylko ze jest rownoramienny To wychodzi z obliczen .No chyba że się myle . j Jesli tak to przepraszam

Legend of whitesnake : Dobrze . Już widzę . Wiem o co chodzi Tak masz rację . Przyznaję mój bład .

πesio: Spokojnie, wyluzuj W treści nie jest napisane,że odcinek AC jest średnicą! ( a na Twoim rys. jest

Legend of whitesnake : Po prostu nie pomyślałem . Samo sie tak jakos narysowało

Podróba podróby 6-latka:

Legend of whitesnake : Oglądałem kiedyś chiński serial o tym samym tytule i tak jakoś mnie się przypomniał

πesio: Powtarzam 10000000000 razy,że: poprawny rysunek,to połowa sukcesu do rozwiązania zadania!

Legend of whitesnake : Wiem πesio Wybacz staremu . Potrafisz , możesz?

Marysia: Dziękuje

πesio: @ Marysia Dokończyłaś?

Legend of whitesnake :

	a2*√3		18√3		9√3
P(ΔABC)=		=		=		[j2] gdzie a=3√2
	4		4		2

	1
P(ΔADC)=		*|AD|*|CD|*sin120o gdzie |AD|=2√3 |CD|=3−√3
	2

	1		1		6(3−√3		3(3−√3
PΔ(ADC)=		*2√3*(3−√3)*√3=		*2√3*√3*(3−√3)=		=		=
	4		4		4		2

	9−3√3
=		[j2]
	2

	9√3		9−3√3		6√3+9
P(ABCD)=		+		=		[j2] .
	2		2		2