W trapezie ABCD, AB II DC Kuba: W trapezie ABCD, AB II DC, przekątne przecinają się w punkcie E. Wiedząc, że pola trójkątów ABE i CDE są odpowiednio równe 90 cm² i 40 cm², oblicz pole trójkąta AED.

chichi: P_ΔAED=√40*90=60 [cm²]

Kuba: To jest wzór?

Kuba: Wiem, że to jest zależność, ale nie miałem tego na lekcjach w 2 liceum Da się to inaczej policzyć?

Nieświęty Franciszek: miałeś podobieństwo trójkątów ? to wyprowadzisz sobie to

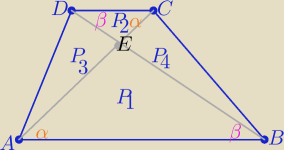
Klara: Z podobieństwa trójkątów ABE i DCE z cechy (kkk) w skali k

	P1
to		=k2
	P2

	√P1
		=k ⇒√P1*P2= k*P2= P3=P4 bo P3=P4=k*P2
	√P2

P(AED)=P₃=P₄= √40*90= 60 i mamy ładne wzorki: P(trapezu)= (√P₁+√P₂)² , P₃=P₂=√P₁*P₂ ==================================

chichi: Fenomenalne nawet bym powiedział

Klara: