Wykaż, że matmix: Wykaż, że stosunek pola koła, do pola trójkąta prostokątnego równoramiennego wpisanego w to koło wynosi π. Potrafię dojść do poprawnego wyniku w tym zadaniu, nie rozumiem natomiast jednego stwierdzenia zaprezentowanego na stronie, z której pochodzi − https://zdajmyto.pl . W rozwiązaniu pojawia się: Ponieważ a>0, to otrzymujemy: a=r√2. a jest długością boku, wiadomo, że dodatnie, a nie ujemne, czy napisanie czegoś takiego jest konieczne? tutaj link bezpośredni do rozwiązania, o którym wspominam − https://zdajmyto.pl/arkusze/4/28 Czy na maturze muszę mając na przykład: r² = 4 i wiedząc wcześniej, że r > 0 muszę pisać r = 2 albo r = −2 i potem pisać, że tylko r = 2 jest ok... ?

wredulus_pospolitus: mamy trójkąt prostokątny wpisany w okrąg −−−> wniosek: przeciwprostokątna = średnicy = 2r mamy trójkąt prostokątny równoramienny −−−> wniosek: boki mają długość a, a, 2r z tw. Pitagorasa mamy więc: a² + a² = (2r)² −−−> wniosek: a = √2r (bo a>0)

wredulus_pospolitus: na maturze mając r² = 4 i widząc, że masz r>0 musisz napisać coś w stylu: r² = 4 wiemy, że r> 0 r = 2

wredulus_pospolitus: jednak równie dobrze możesz napisać: r² = 4 r = 2 lub r = −2 (nie należy do dziedziny rozwiązań / sprzeczne, r>0)

matmix: dziękuję za obszerne wyjaśnienie

Klara:

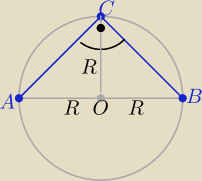
	1
Pk= πR2 , P(ΔABC)=		*2R*R = R2
	2

Pk		πR2
	=		=π
PΔ		R2

i po ptokach

matmix: ooo i to jest fajne rozwiązanie! Dzięki!