Twierdzenie
Don't For Me:
Udowodnić twierdzenie :
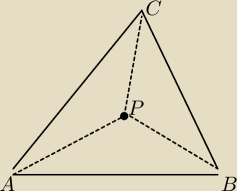
Jeżeli P jest punktem wewnętrzym trójkąta ABC , to suma odległości punktu P od wierzchołków
trójkąta ABC jest mniejsza od jego obwodu
Wskazówka . Skorzystać z pewnika 11.
AP<PC+AC
AP<PB+AB
PC<PB+BC
PC<AP+AC
PB<PC+BC
PB<AP+AB
2AP+2PC+2PB<2PC+2PB+2AP+2AB+2BC+2CA
0<2(AB+BC+CA)
Nie wiem czy to jest dobrze
28 kwi 23:07
chichi:
Dobra wskazówka

28 kwi 23:12
Don't For Me: Postaram się zrobic z tego pewnika zaraz
A to rozwiązanie może byc?
28 kwi 23:15
Klara:
Pewnik 11 jest typu:
Ile lat ma córka ogrodnika?
28 kwi 23:15
Don't For Me: Jutro skończy 29 bo mój przyjaciel jest ogrodnikiem i ma cókę

28 kwi 23:17
Don't For Me: Pewnik11
Każda prosta przechodząca przez wierzcholek trójkąta i punkt leżący wewnątrz trójkąta przecina
bok przeciwległy w punkcie różnym od jego końców
Chciałem zrobić na razie bez tego pewnika
28 kwi 23:21
Don't For Me: Zapytam jeszcze raz
Czy sposób 23:07 jest dobry ?
28 kwi 23:41
Klara:
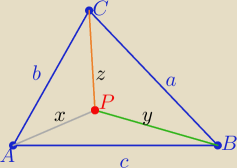
c<x+y
b<x+z
a<y+z
a+b+c < 2(x+y+z)
28 kwi 23:43
Don't For Me: Mialobyc odwrotnie ale dziękuje.
Już przy tym rozwiązaniu sobie poradzę.Bede mial dwa sposoby
Dziękuje jeszcze raz
28 kwi 23:53
 Udowodnić twierdzenie :
Jeżeli P jest punktem wewnętrzym trójkąta ABC , to suma odległości punktu P od wierzchołków
trójkąta ABC jest mniejsza od jego obwodu
Wskazówka . Skorzystać z pewnika 11.
AP<PC+AC
AP<PB+AB
PC<PB+BC
PC<AP+AC
PB<PC+BC
PB<AP+AB
2AP+2PC+2PB<2PC+2PB+2AP+2AB+2BC+2CA
0<2(AB+BC+CA)
Nie wiem czy to jest dobrze
Udowodnić twierdzenie :
Jeżeli P jest punktem wewnętrzym trójkąta ABC , to suma odległości punktu P od wierzchołków
trójkąta ABC jest mniejsza od jego obwodu
Wskazówka . Skorzystać z pewnika 11.
AP<PC+AC
AP<PB+AB
PC<PB+BC
PC<AP+AC
PB<PC+BC
PB<AP+AB
2AP+2PC+2PB<2PC+2PB+2AP+2AB+2BC+2CA
0<2(AB+BC+CA)
Nie wiem czy to jest dobrze


 c<x+y
b<x+z
a<y+z
a+b+c < 2(x+y+z)
c<x+y
b<x+z
a<y+z
a+b+c < 2(x+y+z)