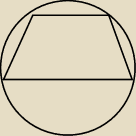
optymalizacja damn_ik: Z arkusza blachy w kształcie półkola o promieniu R należy wyciąć trapez, którego jedna podstawa jest średnicą tego półkola, a wierzchołki drugiej podstawy leżą na jego brzegu (zobacz rysunek) Oblicz jaką długość powinno mieć ramię tego trapezu, aby jego pole było największe możliwe. Oblicz to pole. Mam problem z rozgryzieniem tego trapezu, wiadomo, że jest to równoramienny, h to będzie z pitagorasa z trójkąta 1/2R, h i ramię c ?

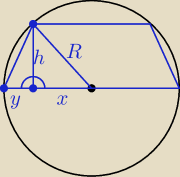
Szkolniak: A może teraz coś?

ICSP: Dlaczego uważasz, że to trapez równoramienny będzie miał największe pole?

Szkolniak: A nie da się wykazać tego, że trapez wpisany w okrąg jest zawsze trapezem równoramiennym? Wynika to z warunku na możliwość wpisania czworokąta w okrąg.

Japońska podróba 6-latka: a na nierównoramiennym da się okrąg opisać?

ICSP: Już mi się coś w tej głowie p******i

Japońska podróba 6-latka: instalacja ci się przegrzewa , za bardzo procesor na overclockingu chodzi

ICSP:

	1
P =		R2(2sinα + sinβ)
	2

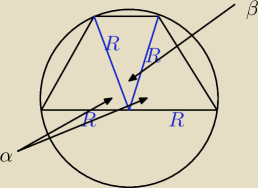
przy czym 2α + β = π Wystarczy znaleźć maksymalną wartość funkcji w nawiasie. przy wskazanym warunku. Wyjdą trzy trójkąty równoboczne.

Szkolniak:

	√3
W sumie zrobiłem tak jak pisałem i wychodzi ładnie, bo h=		R itd., ale jedynie pochodna
	2

mnie zastanawia, bo wychodzi f(h)=Rh+√R²h²−h⁴ Da się taką pochodną policzyć metodami szkolnymi? Jak połączyć taką sumę z pierwiastkiem?

damn_ik: Rh pod pierwiastek wrzucamy, tworzymy funkcję pomocniczą, czyli odpuszczamy sobie ten pierwiastek i liczymy normalnie pochodną

damn_ik: a nie kurde, tam jest jednak dodawanie xd

Szkolniak: No dokładnie, dlatego mnie to zastanawia co w takiej sytuacji trzeba by było zrobić na maturze jak ktoś nie umie pochodnej z pierwiastka? Dlatego ja bym polecał się nauczyć na maturę, bardzo dużo wychodzi zadań z pierwiastkiem we wzorze i wydaje mi się że jest to po prostu wygodniejsze, a nie jest też takie trudne do liczenia..

Louie314: Można też z tego rysunku ułożyć funkcję zmiennej x i wyjdzie iloczyn pod pierwiastkiem, ale i tak sprowadza się to do policzenia pochodnej funkcji złożonej (w ostateczności można wymnożyć nawiasy i wtedy obliczyć pochodną wielomianu).

damn_ik: @Szkolniak jaki ci wyszedł wzór na pole? bo mam h²=x*y R=x+y czegos mi chyba brakuje..

Szkolniak:

	2R2h−4h3
U mnie wyszło f(h)=Rh+√R2h2−h4 −> y'=R+
	2√R2h2−h4

Szkolniak:

	2R−b
U nas 'a' (dolna podstawa trapezu) równa jest 2R, y równe jest		i x+y=R, stąd
	2

	b
x=
	2

Teraz z trójkąta prostokątnego, w którym przyprostokątne to x i h, a przeciwprostokątna to R: x²+h²=R²

	b2
		+h2=R2
	4

b²+4h²=4R² b=2√R²−h² No i podstawiłem do wzoru na pole trapezu:

	(a+b)h		2R+2√R2−h2
P=		=		h
	2		2

P(h)=h(R+√R²−h²) + dziedzina

damn_ik: ok, już jasne wszystko

Szkolniak: Zastanawiam się tylko jeszcze co do dziedziny, bo po przyrównaniu pochodnej to zera wychodzi nam równanie:

	2h2−R2
R=		/ podnosimy do kwadratu, bo R>0 i z początku założenie, że to co pod
	√R2−h2

pierwiastkiem jest dodatnie, czyli h<R

	√2
A co do licznika to nie powinniśmy też zrobić założenia, że 2h2−R2 ⇔ h>		R?
	2

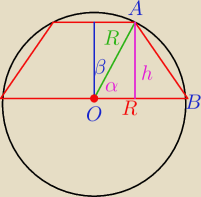
janek191: 0 < α < 90^o α + β = 90^o

h
	= sin α ⇒ h = R sin α
R

Pole trapezu P = 2*( 0,5 R² sin α + 0,5 h R sin β ) sin β = sin ( 90⁰ − α) = cos α więc P = R²*( sin α + sin α*cos α) = = R² *( sin α + 0,5 sin 2α) P ' = R²*( cos α + cos 2α) P'(α) = 0 ⇔ cos α + cos2α = 0 cos α = − cos 2α = − ( cos²α −1) 2 cos²α + cos α − 1 = 0 Δ = 9 cos α = −1 − odpada lub cos α = 0,5 wtedy α = 60^o więc Δ AOB jest równoboczny, zatem AB = R

Louie314: Z rysunku Szkolniaka: h²+x²=R² ⇒ h=√R²−x² a=2R b=2x Zatem:

	2R+2x
P=		*√R2−x2=(R+x)√(R−x)(R+x)=√(R+x)3(R−x)
	2

Wystarczy, że rozpatrzymy funkcję: f(x)=(R+x)³(R−x) Obliczamy pochodną: f'(x)=3(R+x)²(R−x)+(R+x)³=(R+x)²(3(R−x)+R+x)=(R+x)²(4R−2x)=2(R+x)²(2R−x) Zerujemy ją: 2(R+x)²(2R−x)=0

	R
x=−R (odpada, bo wtedy x<0) lub x=
	2

	R
W punkcie x=		funkcja przyjmuje maksimum lokalne.
	2

Stąd: x+y=R

R
	+y=R
2

	R
y=
	2

Obliczamy długość ramienia trapezu o możliwie największym polu:

	R		R
c2=h2+y2=R2−(		)2+(		)2=R2
	2		2

c=R