planimetria Kajetan: Dany jest romb ABCD. Przez wierzchołki B i D poprowadzono dwie proste równoległe przecinające boki CD i AB − odpowiednio − w punktach M i N, tak, że podzieliły one ten romb na trzy figury AND, NBMD, BCM o równych polach. Ponadto wiadomo, że |MB| = |ND| = |BD|. Oblicz cosinus kąta ostrego tego rombu.

Louie314:

	5
Wyszło mi cosα=		.
	6

Kajetan: a jak do tego sie zabrales? ja zrobilem rysunek, ale kompletnie nie wiem jak to ruszyc ...

Louie314: Bazuj na polach. Przyjmij sobie np. |DM|=x, bok rombu np. |AB|=a i wysokość rombu jako h. Przyrównaj pole trójkąta AND (BCM) z polem równoległoboku NBMD (mają takie same wysokości). Dzięki temu wyrazisz "a" za pomocą x. Potem musisz jeszcze wykombinować coś, aby wyznaczyć "h" przy pomocy "x" (lub a). A cosinus policzysz łatwo z pola rombu, ponieważ jest ono równe a²sinα i składa się z pól dwóch trójkątów i równoległoboku.

Kajetan: ok, dzieki! juz sie za to zabieram

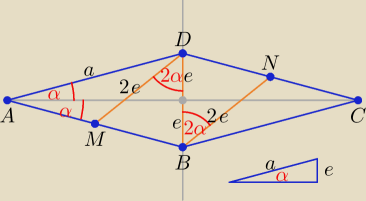
qstosz: Pola P_AMD = P_MBND = P_BCN = P i P_ABCD = 3P = a²sin(2α)

	1
P = 2*		*2e*2e*sin(2α) = 4e2sin(2α), 3*4e2sin(2α) = a2sin(2α) stąd a = 2√3e
	2

	e
sinα =		, cos2α = 1 − 2sin2α
	a

Kajetan: Louie314 bardzo dziekuje za wskazowki! wszystko pieknie wyszlo !