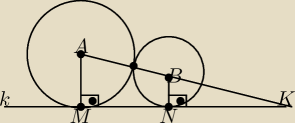
 Dane są średnice długości 2m i 2n m>n
Jak wyznaczyć pole trójkata MAK
Dane są średnice długości 2m i 2n m>n
Jak wyznaczyć pole trójkata MAK
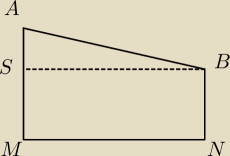 |AB| = m +n
|SB| = |MN|
|SA| = m − n
z twierdzenia Pitagorasa:
|SA|2 + |MN|2 = |AB|2
(m−n)2 + |MN|2 = (m + n)2
stąd znajdziesz |MN|
twierdzenie talesa lub też podobieństwo trójkątów: ΔAMN , ΔNBK
pozwoli znaleźć |NK|
|AB| = m +n
|SB| = |MN|
|SA| = m − n
z twierdzenia Pitagorasa:
|SA|2 + |MN|2 = |AB|2
(m−n)2 + |MN|2 = (m + n)2
stąd znajdziesz |MN|
twierdzenie talesa lub też podobieństwo trójkątów: ΔAMN , ΔNBK
pozwoli znaleźć |NK|
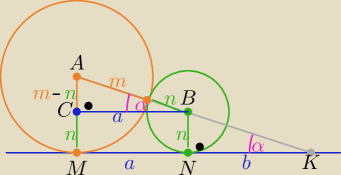 Z treści zadania długości promieni tych okręgów
|AM|=m i |BN|=n , m>n
to
|AB|=m+n, |AC|=m−n , |MN|=CB|=a , |NK|=b
Z treści zadania długości promieni tych okręgów
|AM|=m i |BN|=n , m>n
to
|AB|=m+n, |AC|=m−n , |MN|=CB|=a , |NK|=b
| 1 | ||
P(ΔMAK)= | m*(a+b) | |
| 2 |
| a+b | m | am | ||||
= | ⇒ a+b= | =......... | ||||
| a | m−n | m−n |
| m2√mn | ||
P(MAK)= | ||
| m−n |