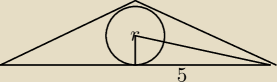
trygonometria kris: Trygonometria. w trójkąt równoramienny abc o kącie między ramionami 150 i podstawie ab=10, wpisano okrąg. Oblicz promien okręgu ^r₅=tg 15 ^r₅=0,268 r=1,34 dobrze czy źle ?

chichi: Kąt między ramionami ma 150^o → kąty przy podstawie mają po 15^o, środek okręgu wpisanego w trójkąt znajduje się w punkcie przecięcia się dwusiecznych, więc czy aby na pewno tan(15^o)?

kris: oczywiscie tg 7,5 ale taki sposob jest dobry oprócz oczywisćie tego błedu

Anawa: Tylko jak policzysz tg7,5^o?

chichi: Tak, tan(7.5^o)=√6+√2−√3−2

Anawa: A tak bez popisu ?

ICSP: Przecież widzisz, że kris wziął przybliżoną wartość z tablic. Zrób to samo.

chichi:

	1−cos(45o−30o)
@6latek jakiego znowu popisu? tan(7.5o)=
	sin(45o−30o)

Louie314:

	2tgα
tg2α=
	1−tg2α

	2tg(15)		√3
tg(2*15)=		=
	1−tg2(15)		3

Stąd: tg(15)=2−{3}

	2tg(7.5)
tg(2*7.5)=		=2−√3
	1−tg2(7.5)

Stąd:

	1−2√2−√3
tan(7.5)=		=√6+√2−√3−2
	√3−2

chichi: Inny sposób:

	1		1
(1) P=		*a2*sin(150o) ∧ P=		*a*10*sin(15o) ⇒ a=5√6−5√2
	2		2

(2) p=5√6−5√2+5

	1
(3) P=		(5√6−5√2)2*sin(150o)=50−25√3
	2

(4) (5√6−5√2+5)r=50−25√3 ⇒ r=5√6+5√2−5√3=10

Anawa: Ja wiem jak obliczyć .Znam wzory połókowe Natomiast jest pytanie czy kris wie jak obliczyć ? Moje pytanie było właśnie skierowane do niego do niego

chichi: r=5√6+5√2−5√3−10

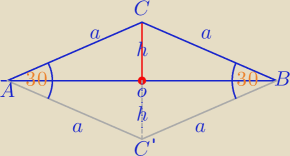
Mila: Unikamy wartości funkcji tryg. kątów 15^o, 75^o, 7.5^o 1)

	a2
PΔ=
	4

2) W ΔCOB: h²=a²−25 /*4 4h²=4a²−100 3) W ΔCAC': z tw. cosinusów 4h²=a²+a²−2 a²cos 30^o a²=100*(2−√3)

	√2		10√4−2√3
a=10√2−√3 ⇔a=10√2−√3*		=
	√2		√2

	√(√3−1)2
a=10*
	√2

a=5*(√6−√2) 4) p=5*(√6−√2+1)

a2
	=5*(√6−√2+1)*r
4

	1
100*(2−√3)*		=5*(√6−√2+1)*r
	4

	5*(2−√3)
r=
	√6−√2+1

==========