26 kwi 19:54
26 kwi 19:56
jc:
cos(6π − π/6)= cos(−π/6)=cos π/6 = √3 /2
sin(6π − π/6) = sin(−π/6)= − sin π/6 = − 1/2
26 kwi 20:25
anonim123: Ale skąd mam wiedzieć że są w 4 ćwiartce?
26 kwi 20:36
Anawa: Ech.
A gdzie leży punkt w układzie współrzędnych ktorego współrędna xowa jest dodatnia , a
współrzęna yowa jest ujemnna ?
W której ćwiartce ?
26 kwi 20:49
anonim123: W czwartej ale skąd wiesz że współrzędna x jest dodatnia a y ujemna?
26 kwi 20:57
Anawa:
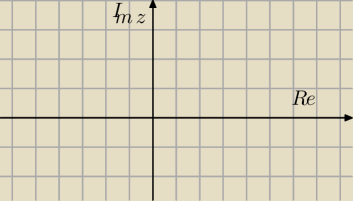
z=x+iy
26 kwi 21:02
anonim123:
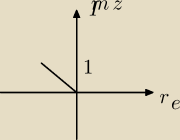
To dlaczego my na lekcjach zaznaczaliśmy przy tym przykładzie re= −
√3 a Imz =1
26 kwi 21:07
anonim123: przy przedstawianiu liczby z=− √3+i w postaci trygonometrycznej
26 kwi 21:09
Anawa: Dostaniesz taką liczbe
z= 64
√3−i64
26 kwi 21:09
anonim123: Nie rozumiem tego fragmentu z ćwiartkami nadal

26 kwi 21:12
anonim123: ale przed obliczeniem tej liczby muszę wiedzieć która to ćwiartka
26 kwi 21:13
Anawa: Proszę wybaczyć ale to szkoła podstawowa .
Przecież −
√3 jest liczba ujemna ≈−1,73 więc zaznaczasz na ujemnej częsci osi re
i=1 zaznaczasz na dodatniej części osi Imz
Teraz
64
√3 jest dodatnie wiec na dodatniej cześci osi Re
| | 1 | |
−i |
| jest ujemne ( bo przy i jest (−) więc na ujemnej częsci osi Imz |
| | 2 | |
26 kwi 21:18
Anawa: Tak się zastanawiam . Do czego Ci potrzebna jest wiadomość przy potęgowaniu do której ćwiartki
należy liczba którą będziesz potęgowac?
Myślę że bardziej potrzebna wiedza ze wzorów redukcyjnych i okresowości funkcji sinus i cosinus
26 kwi 21:23
anonim123: bo miałam tam zapisane że to jest 4 ćwiartka i korzystamy z własności z rymowanki o ćwiartkach
więc
myślałam że to istotne
26 kwi 21:25
anonim123: | | 1 | |
Anawa ale to co piszesz czyli 64 √3 oraz −i |
| nie są znane w tym momencie o który mi |
| | 2 | |
chodzi
26 kwi 21:32
Anawa: Nie mam już sił.
Napiszę jeszcze raz . Nie jest mi potrzebna wiedza żeby spotegować liczbe zespoloną w której
ćwiartce ona leży .
26 kwi 21:42
anonim123: To napisz jak to trzeba obliczyć inaczej?
26 kwi 21:46
jc: O co chodzi z tymi ćwiartkami? W treści zadania jest coś o ćwiartkach?
26 kwi 21:51
ICSP: Styl nauczania.
Aby przekształcić liczbę zespoloną z postaci kanonicznej do trygonometrycznej zaczyna się od
znalezienia ćwiartki w której ta liczba się znajduje.
Dziwne podejście.
26 kwi 21:56
jc: Ale przecież określenie ćwiartki może daje dokładność 45o. Może już lepsze byłyby rumby?
26 kwi 22:00
chichi:
W I ćwiartce same plus, w II plus ma sinusów, w III tangens i cotangens, a w IV cosinus

Takie wierszyka mnie w szkole uczyli

26 kwi 22:06
ICSP: Tutaj nie do końca chodzi o dokładność tylko bardziej o sposób.
Pierwszym etapem jest zlokalizowanie ćwiartki w której znajduje się dana liczba zespolona.
Następnie znajdujesz cosφ gdzie φ jest argumentem.
Są zazwyczaj dwie opcje:
nie ma znaczenia czy przed ułamkiem znajduje się minus czy nie.
Interesuje nas tylko licznik.
| | tajemnicze coś | |
Jeżeli w liczniku jest 1 (przypadek 1o) to kąt jest w postaci: φ = |
| |
| | 3 | |
| | tajemnicze coś | |
natomiast w przypadku 2o kąt jest w postaci: φ = |
| |
| | 6 | |
Na koniec należy tak wybrać tajemnicze coś aby kąt wskoczył do odpowiedniej ćwiartki (dlatego
ją wyznaczalismy) oraz aby przez przypadek licznik nie skrócił się z mianownikiem.
Nie potrafię wyjaśnić dlaczego tak się to robi.
26 kwi 22:14
Anawa: To ma napisane na kartce

| | 5 | | 5 | |
Mam już liczbę zespoloną z=2(cos |
| π+isin |
| π) w postaci trygonometrycznej która sie |
| | 6 | | 6 | |
nadaje do potęgowania więc napisałem że nie interesuje mnie w której ona leży .
Stosuję tylko odpowiedni wzór.
Natomiast jeśli bym miał liczbę zespoloną w postaci kartezjańskiej to wtedy potrzebna mi jest
wiedza w ktorej ona leży ćwiartce gdyż muszę ustalić argument φ aby tą liczbę przekształcić
do postaci trygonometrycznej
O to chodzi? ,
26 kwi 22:22
jc:
2+3i leży w pierwszej ćwiartce, a w czym ta wiedza pomaga?
26 kwi 22:37
ABC: panowie o czym wy rozmawiacie ... ćwiartka na dwóch to jest nic, pół litra na trzech to też nic

26 kwi 22:43
Anawa: Pół litra na dwóch jest w sam raz
Pod warunkiem że pije jeden

26 kwi 22:47
Anawa: z=2+3i
|z|=
√22+32=
√13
z=
√13(cos 56
o 19'+isin 56
o19' )
26 kwi 22:59
anonim123: A można to policzyć ze wzorów redukcyjnych bo w tych ćwiartkach się gubię?
27 kwi 11:18
 z=x+iy
z=x+iy
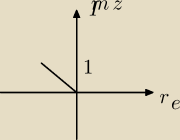 To dlaczego my na lekcjach zaznaczaliśmy przy tym przykładzie re= − √3 a Imz =1
To dlaczego my na lekcjach zaznaczaliśmy przy tym przykładzie re= − √3 a Imz =1

 Takie wierszyka mnie w szkole uczyli
Takie wierszyka mnie w szkole uczyli 


