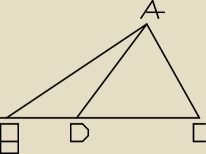
Dowod Nolan82: Mam taki dowod i probowalem juz chyba wszystkiego. Udowodnij że AD²=BD*BC wiedzac ze kat ACB ma miare 66 stopni, kat BAD 18 stopni, a kat ABC 30 stopni.

chichi:

	a+b		a
ΔECB ∼ ΔEBD ⇒		=		⇒ a2=b(a+b) □
	a		b

Nolan82: A skad tu sie niby nagle tyle wszystkiego wzielo na tym rysunku?

Nolan82: To chyba nie jest dobrze albo ja tego nie czaje moze ktos zrobi inaczej dziekuje

chichi: A co Ci tu nie pasuje?

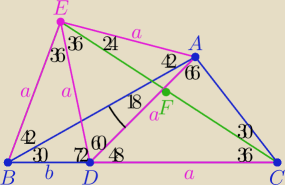
πesio: Mamy trzy trójkąty podobne : ΔABC, ΔAFE ,ΔBFD z cechy (kkk)

	a+b		a
to		=
	a		b

a²=b(a+b) |AD|²=|BD|*|BC| ============

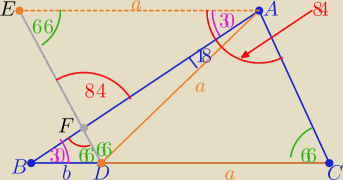
πesio: Oczywiście : |∡BAC|=84^o ( za bardzo wysunął mi się łuk czerwony na rysunku

chichi: "A skad tu sie niby nagle tyle wszystkiego wzielo na tym rysunku?" "To chyba nie jest dobrze" @Eta pytanie po co robić, po co się wysilać jak autor powie, że źle bo nie rozumie rozwiązania jednolinijkowego

Saizou : Brzydki dowód geometryczny Wyznaczymy sin18^o. Niech x = 18^o, wówczas 90 = 18*5 = 5x 90 = 3x + 2x 90−3x = 2x sin(90−3x) = sin(2x) cos(3x) = sin(2x) 4cos³x−3cosx = 2sinxcosx 4cos²x−3 = 2sinx 4(1−sin²x) − 3 =2sinx 4sin²x+2sinx−1=0 sinx = t , t > 0 4t²+2t−1=0 Δ = 4+16 = 20 →√Δ = 2√5

	2−2√5		1−√5
t1 =		=		< 0
	8		4

	2+2√5		1+√5
t2 =		=
	8		4

	1+√5
sin18o =
	4

I teraz z tw. sinusów

a		b
	=
sin18o		sin30

Wyznaczamy a w zależności od b i sprawdzamy czy zachodzi równość a² = b(a+b)

πesio:

Saizou : Dlatego brzydki