Trójkąt prostokątny, środkowe Szkolniak: Wykaż, że w trójkącie prostokątnym o bokach długości a, b, c suma kwadratów długości jego środkowych jest równa 150% kwadratu długości przeciwprostokątnej. I napotykam na problem, bo ciągle wychodzi mi jakaś nieprawda, że 5(a²+b²)=6(a²+b²) i zastanawiam się czy to co mamy wykazać jest w ogóle prawdą? Jeśli będzie trzeba to zamieszczę swoje rozwiązanie w celu znalezienia błędu (którego nie widzę po trzykrotnym przejrzeniu..)

chichi: a,b − przyprostokątne i c − przeciwprostokątna, zatem c²=a²+b² Ze wzoru na środkową:

	1
ma=		(2b2+2c2−a2)
	4

	1
mb=		(2a2+2c2−b2)
	4

	1
mc=		(2a2+2b2−c2)
	4

+ _________________________

	3		3		3
ma+mb+mc =		(a2+b2+c2) =		(2c2) =		c2 ⬠
	4		4		2

chichi: zapomniałem o kwadratach z rozpędu, powinno wszędzie być m_a², m_b² i m_c²

Szkolniak: Widzisz.. ja z rozpędu kompletnie zapomniałem o trzeciej środkowej i nie wiem czemu poprowadziłem tylko dwie, do przyprostokątnych Dzięki wielkie, już pasuje

chichi: Trzy razy przeglądałeś i nie zauważyłeś?

chichi: A skąd zadanie swoją drogą?

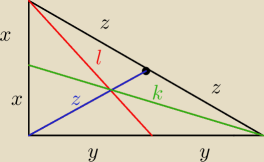
Saizou : Albo tak l² = 4x²+y² k² = 4y²+x² 4z² = 4x²+4y² → z² = x² + y² ================================+ l²+k²+z² = 6x² + 6y² = 6(x²+y²) = 6z²

	1
z =		c
	2

	1
l2+k2+z2 = 6x2 + 6y2 = 6(x2+y2) = 6z2 = 6*		c2 = 1,5c2
	4

Szkolniak: No bo nie pomyślałem nawet że może brakować tej trzeciej środkowej, przekonany byłem że chodzi tylko o te dwie Zadanie od nauczyciela sprzed 2 lat, nie mam pojęcia skąd je wziął, bo mam na liście Saizou dokładnie w ten sposób zrobiłem dla tych dwóch środkowych tylko że potem mi wychodziła jakaś bzdura, dzięki również

Saizou :