Elipsa Werka: Hejka! Mam takie zadanie z działu elipsa: Znalejdź równanie drogi punktu M, któregoodległość podczas ruchu jest trzykrotnie większa od x = 9 niż od A(1,0). Moim tokiem myślenia i dzięki mojemu szkicowi doszłam do tego, że: odległość punktu A od prostej to 9−1 = 0, przyjmuję też, że środek elipsy S=A, czy to złe założenie? Dzięki temu otrzymuję b+3b = 8 => b=2 jednym z punktów elipsy jest (3,0) podstawiam do równania elipsy i otrzymuję, że a=2 a więc moje równanie elipsy to x²/4 + y²/4 = 1 jednak w odpowiedziach z tyłu książki jest wynik 8x²+9y²=72 Czy mogę prosić o wskazówkę?

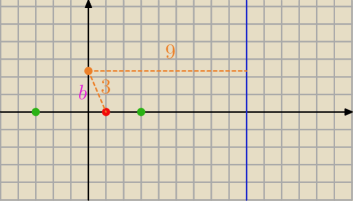
wredulus_pospolitus: Przecież Tobie wyszedł okrąg x² + y² = 4 co z oczywistych względów jest błędną odpowiedzią. Patrz zielone punkty należą do elipsy, ponieważ: (8−x) = 3x −−> x = 2 (prawy punkt) (8+x) = 3x −−−> x = 4 (lewy punkt) stąd mamy środek elipsy jest w punkcie (0,0). Pozostaje wyznaczyć współrzędną pomarańczowego punktu elipsy ... czyli wyznaczenie 'b' elipsy b² = 9 − 1 = 8 natomiast a = 3 −> a² = 9 no i mamy:

(x−0)2		(y−0)2		x2		y2
	+		= 1 −−>		+		= 1
a2		b2		9		8

lub jak w książce 8x² + 9y² = 72 (mnożymy po prostu obustronnie przez 72)

Werka: dziękuję bardzo, już rozumiem!