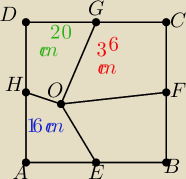
 Dany jest kwadrat ABCD. Punkty E, F, G, H są odpowiednio środkami boków AB, BC, CD, AD. W
środku kwadratu wybrano punkt O, poprowadzono odcinki EO, FO, GO oraz HO, tworząc czworokąty
AEOH, HOGD i GOFC o polach równych 16 cm2, 20 cm2 i 36 cm2 (rysunek). Oblicz długość boku
kwadratu ABCD.
Dany jest kwadrat ABCD. Punkty E, F, G, H są odpowiednio środkami boków AB, BC, CD, AD. W
środku kwadratu wybrano punkt O, poprowadzono odcinki EO, FO, GO oraz HO, tworząc czworokąty
AEOH, HOGD i GOFC o polach równych 16 cm2, 20 cm2 i 36 cm2 (rysunek). Oblicz długość boku
kwadratu ABCD.
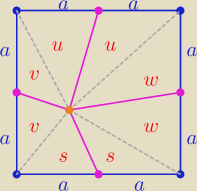 u+w=36
u+v=20
− −−−−−
w−v= 16
i s+v= 16
+ −−−−−−−−
w+s = 32
to pole kwadratu : P= 20+36+16+32= 104 = 4a2
więc dł. boku kwadratu
2a=2√26
=========
u+w=36
u+v=20
− −−−−−
w−v= 16
i s+v= 16
+ −−−−−−−−
w+s = 32
to pole kwadratu : P= 20+36+16+32= 104 = 4a2
więc dł. boku kwadratu
2a=2√26
=========