Stereometria
Tomasz:
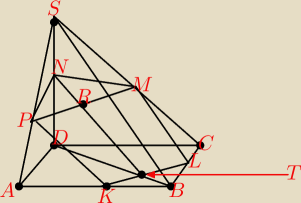
Podstawą ostrosłupa ABCDS jest kwadrat ABCD o boku długości 2
√2. Krawędź boczna DS jest
wysokością tego ostrosłupa, a jej długość jest równa 8. Ostrosłup przecięto płaszczyzną
przechodzącą przez punkty K, L i N, które są odpowiednio środkami krawędzi AB, BC, DS.
Otrzymany w ten sposób przekrój to pięciokąt KLMNP (rysunek). Przekątna PM tego pieciokąta
oraz odcinek TN łączący wierzchołek ze środkiem przeciwległego boku KL przecinają się w
punkcie R. Oblicz odległość R od przekątnej BD.
Wyszło mi 10/3 i zastanawiam się czy dobrze. Ten rysunek mógł wyjść trochę krzywo − ten R to
powinien być chyba nad spodkiem wysokości chyba? (czy da się to udowodnić)?
 Podstawą ostrosłupa ABCDS jest kwadrat ABCD o boku długości 2√2. Krawędź boczna DS jest
wysokością tego ostrosłupa, a jej długość jest równa 8. Ostrosłup przecięto płaszczyzną
przechodzącą przez punkty K, L i N, które są odpowiednio środkami krawędzi AB, BC, DS.
Otrzymany w ten sposób przekrój to pięciokąt KLMNP (rysunek). Przekątna PM tego pieciokąta
oraz odcinek TN łączący wierzchołek ze środkiem przeciwległego boku KL przecinają się w
punkcie R. Oblicz odległość R od przekątnej BD.
Wyszło mi 10/3 i zastanawiam się czy dobrze. Ten rysunek mógł wyjść trochę krzywo − ten R to
powinien być chyba nad spodkiem wysokości chyba? (czy da się to udowodnić)?
Podstawą ostrosłupa ABCDS jest kwadrat ABCD o boku długości 2√2. Krawędź boczna DS jest
wysokością tego ostrosłupa, a jej długość jest równa 8. Ostrosłup przecięto płaszczyzną
przechodzącą przez punkty K, L i N, które są odpowiednio środkami krawędzi AB, BC, DS.
Otrzymany w ten sposób przekrój to pięciokąt KLMNP (rysunek). Przekątna PM tego pieciokąta
oraz odcinek TN łączący wierzchołek ze środkiem przeciwległego boku KL przecinają się w
punkcie R. Oblicz odległość R od przekątnej BD.
Wyszło mi 10/3 i zastanawiam się czy dobrze. Ten rysunek mógł wyjść trochę krzywo − ten R to
powinien być chyba nad spodkiem wysokości chyba? (czy da się to udowodnić)?