W urnie są 2 kule czarne i 3 białe. Wyjmujemy losowo z urny po jednej kuli dotąd, dopóki nie
wyciągniemy kuli czarnej, po czym przerywany doświadczenie. Niech X oznacza ilość wyciągniętych
kul. Podać funkcję prawdopodobieństwa tej zmiennej losowej.
Take coś wymyśliłem,ale nie wiem czy to dobrze,bo mi się coś wydaje,że tu zastosowanie rozkładu
Pascala by sie nadal ale nie wiem jak.
X − ilość wyciągniętych kul
2C,3B (2 czarne,3 białe)
Zdarzenia sprzyjające − A
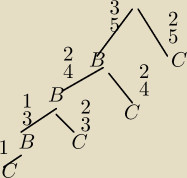
A = C,BC,BBC,BBBC
| 2 | ||
P(C) = | ||
| 5 |
| 3 | 2 | 6 | ||||
P(BC) = | * | = | ||||
| 5 | 4 | 20 |
| 3 | 2 | 2 | 12 | |||||
P(BBC) = | * | * | = | |||||
| 5 | 4 | 3 | 60 |
| 3 | 2 | 1 | 6 | |||||
P(BBBC)= | * | * | = | |||||
| 5 | 4 | 3 | 60 |
)
x = xk |1 |2 ..... −>liczba kul
______ |________ |__
| 2 | 6 | |||
P(x=xk | | | | .... −> prawdopodobieństwo | ||
| 5 | 20 |