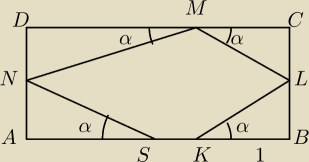
 Na bilardzie ABCD (prostokąt) w punkcie K leży bila. Znajdź kąt α pod jakim bila odbijając się
od
BC, DC, AD, wpadnie do środka AB (czyli S)
|KB|=1
|AB|=2,5
|BC|=1
S− środek |AB|
"kąt padania jest kątem odbicia"
odpowiedź powinna wyjść ctgα=1912 (nie wiem jak do niej dojść, dlatego proszę o pomoc i
opis krok po kroku, jeżeli to możliwe)
Na bilardzie ABCD (prostokąt) w punkcie K leży bila. Znajdź kąt α pod jakim bila odbijając się
od
BC, DC, AD, wpadnie do środka AB (czyli S)
|KB|=1
|AB|=2,5
|BC|=1
S− środek |AB|
"kąt padania jest kątem odbicia"
odpowiedź powinna wyjść ctgα=1912 (nie wiem jak do niej dojść, dlatego proszę o pomoc i
opis krok po kroku, jeżeli to możliwe)
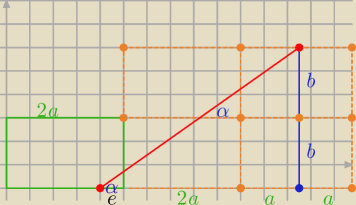
| 2b | ||
tgα= | ||
| d+3a |
| 12 | ||
tgα= | ||
| 19 |
| 2b | ||
tgα= | ||
| e+3a |
| 12 | ||
tgα= | ||
| 19 |
| 19 | ||
to ctgα= | ||
| 12 |
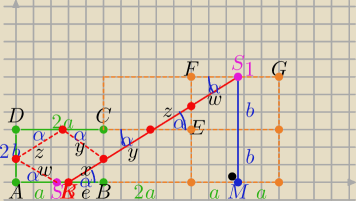 K −− punkt w którym znajduje się bila
Rys. w skali 2:1 |AB|=2a=5 , |KB|=e=2 i |BC|=b=3
Droga ( dł.łamanej) jaką przebędzie bila zanim wpadnie
do środka S odcinka AB :
x+y+z+w = |KS1| −−− dł. przeciwprostokątnej w ΔKS1M
w tym trójkącie
K −− punkt w którym znajduje się bila
Rys. w skali 2:1 |AB|=2a=5 , |KB|=e=2 i |BC|=b=3
Droga ( dł.łamanej) jaką przebędzie bila zanim wpadnie
do środka S odcinka AB :
x+y+z+w = |KS1| −−− dł. przeciwprostokątnej w ΔKS1M
w tym trójkącie
| |S1M| | 2b | |||
tgα= | = | |||
| |KM| | e+3a |
| 12 | 19 | |||
tgα= | lub ctgα= | |||
| 19 | 12 |
