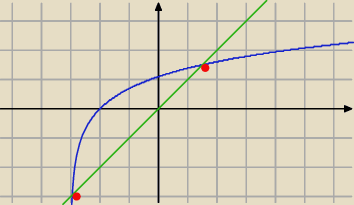
Punkty przecięcia z osią OX Jack: Jak obliczyć miejsca zerowe tej funkcji? y(x)=x−ln(x+3)

a7: 0=x−ln(x+3) x=ln(x+3) ?

Louie314: y(x)=x−ln(x+3) Dziedzina: x+3>0 ⇒ x>−3 x−ln(x+3)=0 ln(x+3)=x ln(x+3)=ln(e^x) x+3=e^x I tutaj musiałbyś znać funkcję specjalną W Lamberta, gdyż zmienna jest i w podstawie, i w wykładniku.

Mariusz: Louie umiesz czytać kod w C bo znalazłem kod źródłowy programu do odwracania macierzy Kod źródłowy był w Pascalu i przełożyłem go na C Sposób ten jest o tyle ciekawy że ma złożoność zbliżoną do eliminacji Gaußa ale nie wymaga dołączania macierzy jednostkowej więc jeśli sprawnie wykonujesz działania arytmetyczne w pamięci pozwoliłaby ci ona zaoszczędzić trochę papieru podczas odwracania macierzy Ja już przećwiczyłem odwracanie macierzy tym algorytmem i kilka macierzy nawet udało mi się odwrócić Przeglądałeś strony ważniaka ? Mają tam dobrze opisany rozkład macierzy na iloczyn LU=PA mimo iż można tam znaleźć kilka literówek to sam sposób przedstawienia tego rozkładu jest dobry dla tego który chciałby zarówno napisać program realizujący taki rozkład jak i samemu go przećwiczyć

Maciess: To jest jakas pasta z tym kodem do odwracania macierzy?

Mariusz: Jeżeli pod pojęciem pasta masz na myśli wklejkę na pastebin.com to tak tam wkleiłem ten kod Kod znalazłem w Pascalu i przełożyłem go na C Tu go masz https://pastebin.com/E0pj4fDS Jak już pisałem jego zaletą jest to że nie trzeba dołączać macierzy jednostkowej

Maciess: Nie. Chodziło mi o to, że od jakiegoś czasu wypytujesz losowe osoby o jakieś kody algorytmów, a żadna nie pyta. Stąd pytanie. Czy to jakis żarcik czy po prostu tak sobie pytasz.

Mariusz: Po prostu mało kto tego algorytmu używa choć jest równie szybki jak eliminacja Gaußa tyle że jest bardziej oszczędny pamięciowo Czasami z góry wiemy że układ równań będzie miał jedno rozwiązanie (przykładowo rozkład na sumę ułamków prostych) i wtedy macierz odwrotna może być wygodna ale myśl sobie co chcesz Nie tak dawno znalazłem u Knutha też pewien algorytm odwracania macierzy https://pdfhost.io/v/gFCD2oWo._Knuth_inverse_matrixpdf.pdf Jak chcesz się wykazać to zamiast pytać o głupoty mógłbyś mi podpowiedzieć jak zapisać go w kodzie