Monotoniczność i ekstrema funkcji.
Jack: Jak zbadać monotoniczność tej funkcji i ekstrema? Obliczyłem dziedzinę, pochodną ale nie mam
pojęcia jak ustalić monotoniczność.
| | √6 | | √6 | |
Dziedzina jej to: x∈(−∞;−2)∪(−2; |
| >∪< |
| ;2)∪(2;∞) |
| | 6 | | 6 | |
| | −24x3−88x | |
Pochodna: |
| |
| | √12x2−2*(x2−4)2 | |
23 kwi 19:44
Louie314: Musisz teraz przyrównać pochodną do zera. Powinno wyjść, że nie posiada miejsc zerowych, zatem
warunek konieczny istnienia ekstremum nie jest spełniony (funkcja nie ma ekstremów). Jeżeli
chodzi monotoniczność, to w takich zadaniach zwyczajowo rysuje się symboliczny wykres
pochodnej. Tutaj nie jest to aż tak łatwe, ale można łatwo określić znak pochodnej na
podstawie jej licznika (gdyż mianownik jest dodatni). Gdy już to zrobisz, to tam gdzie
pochodnia jest większa od 0 − tam funkcja jest rosnąca, a tam gdzie pochodna jest mniejsza od
0 − tam funkcja jest malejąca (w uproszczeniu).
23 kwi 20:05
janek191:
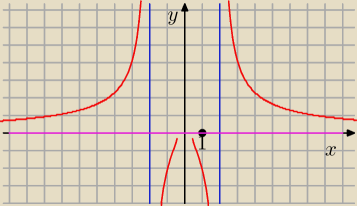
24 kwi 09:38
