proszę o rozwiązanie anna: w prostokącie ABCD punkt E leży na boku AD oraz DE : EA = 1: 2 Odcinek EC przecina się z przekątną DB w punkcie M Wiedząc że pole trójkąta DEM jest równe 2 oblicza) pole trójkąta MBC b)pole trójkąta DBC

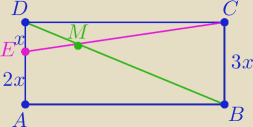
chichi: ΔDEM∼ΔBMC zachęcam do samodzielnego spróbowania, wyznacz skalę i pójdzie

anna: skala to

x		1
	=		P1 =PΔDEM P−2 = PΔMBC
3x		3

P1		1		1
	=		⇒ P2 =2*		= 18
P2		9		9

wyniki to a) 18 b) 24 czy to jest dobrze

blabla:

blabla: no i jest ok

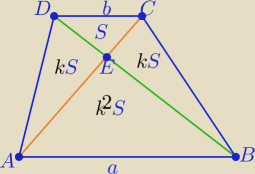blabla: Aniu może Ci się przyda W dowolnym trapezie o podstawach a i b

a
	=k −− skala podobieństwa Δ ABE i DCE
b

Pola : PΔDCE=S , PΔADE=PΔBCE=k*S , PΔABE=k²*S Pole trapezu ; P= (k+1)²*S Np: w trapezie o podstawach 3a i a pole ΔDCE= 5 Oblicz pole trapezu P= (k+1)²*S P= (3+1)²*5 = 16*5= 80

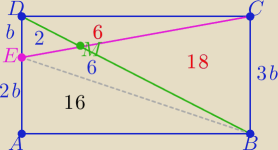
blabla: Dodam,że w tym poprzednim zadaniu z prostokątem czworokąt BCDE jest trapezem o podstawach BC i DE

|BC|
	= 3=k −−− skala podobieństwa
|DE|

i .............

Anawa:

P1		1
	=
P2		9

P₂= 2*9=18

	1
2*		≠18
	9

rucola: P₁=2 , P₂=18

P1		1
	=
P2		9

P₂=2*9=18

	1
18*		=2
	9

rucola: I coTy na to? Anawa

Anawa: A ja na to , ze odniosłem się do wpisu 20 : 10

Anawa: Jeszcze ja na to że też skorzystałęm z wpisów blabla Dziękuje.

rucola: i brakuje.... "pozdrawiam"

Anawa: Pozdrawiam również

anna: blabla jak obliczyłaś że pole Trójkąta BME = 6

blabla: aniu zobacz wpis 20 : 48 (tam wszystko objaśniłam)

blabla: P(ΔBME)= k*P(ΔDEM) = 3*2=6

Anawa: Dlaczego nie patrzysz na rysunek blabla i nie analizujesz co tam jest napisane aniu ?

	3b
k=		=3
	b

PΔBME=k*PΔEMD=3*2=6

anna: dziękuję bardzo za wyjaśnienie