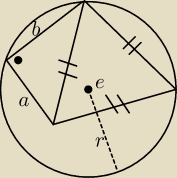
geometria kryspin49: Wyznacz R (na rysunku jest małe bo nie chciało wejść duże) w zależności od a i b. Ten środek okręgu E powinnobyć z dużej nie chciało mi coś wejść a tam gdzie jest kropka miedzy ramionami a i b jest kat prosty zaznaczony ta kropka. Czy ktoś potrafi to rozwiązać?

janek191: Napisz porządnie treść zadania

kryspin49: Wyznacz R w zależności od a i b. Kąt prosty jest między odcinkami a i b i punkt E to środek okręgu.

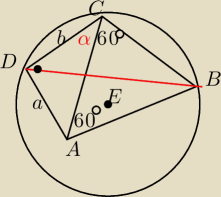
an: Z tw. cosinusów AD, następnie z sinusów średnica

	√(a2+b2)(a2+b2+√3 ab)
R=
	a+√3b

ϱoco: W mianowniku : 2(a+√3b)

chichi: Ja mam taki wynik jak @an, sprawdź swoje obliczenia jeszcze raz

ϱoco: Tak, muszę się cofnąć do podstawówki. Dziękuję.

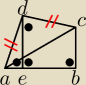
kryspin49: Dziekuje, a mozecie ejszcze zobaczyc takie zadanie? Ile wynosi pole ABCD jeśli |DE|=25, |DC|=|AD| kat ADC=90 stopni

chichi: 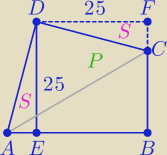P=25²=625

Klara:

kryspin49: a skad my wiemy ze te trojkaciki sa takie same?

chichi: |∡ADC|=90^o ∧ |∡CBA|=90^o → na czworokącie ABCD można opisać okrąg. Niech |∡BAD|=α ⇒ |∡DCB|=180^o−α ⇒ |∡DCF|=α, |∡ADE|=90^o−α=|∡CDF| ΔDCF≡ΔDAE (cecha k−b−k) ⇒ |DE|=|DF|=25 → czworokąt DEBF jest kwadratem o boku 25, a jego pole jest równe polu czworokąta ABCD