zadanie z parametrem Sampas : Dla jakich wartości parametru m dwa różne pierwiastki równania: (m−1)x²+(m+1)x+m−1=0 należą do przedziału (−2,4)? Mam pytanie odnośnie warunków. Ułożyłem je tak:

⎧	m≠1
⎜	(m−1)>0
⎜	Δ>0
⎨	f(−2)>0
⎜	f(4)>0
⎩	−2>p>4

⎧	m≠1
⎜	(m−1)<0
⎜	Δ>0
⎨	f(−2)<0
⎜	f(4)<0
⎩	−2>p>4

I mam pytanie czy można te dwa przypadki połączyć w jeden taki:

⎧	m≠1
⎜	Δ>0
⎨	−2>p>4
⎩	f(−2)f(4)>0

ICSP: −2>p>4 Nie można.

Jolanta: m≠1 Δ>0 pierwiastki róznych znaków x₁*x₂<0

Sampas : p jako odcięta wierzchołka i czemu nie można

Sampas : Jolanta nie muszą być różnych znaków, wystarczy wziąć kontrprzykład 1 i 3

figo: p∊(−2,4)⇒ −2 <p<4

Sampas : aa no tak pomyłka, to teraz dlaczego nie można w jeden przypadek

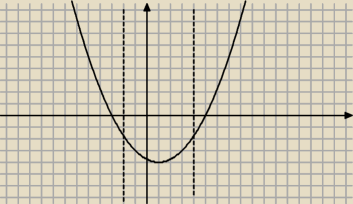
ICSP: Kontrprzykład dla twoich 4 warunków. f(−2)*f(−4) > 0 traci informację o tym czy te wartości są dodatnie czy ujemne. Wiesz tylko, ze są tych samych znaków. Wiem czym jest p. Bardziej chodzi mi o sens logiczny zapisu: −2>p>4

Louie314: Nota bene możesz zrobić relatywnie prostsze warunki: x₁>−2 x₂>−2 x₁+2>0 x₂+2>0 Stąd: x₁+x₂+4>0 i (x₁+2)(x₂+2)>0 Dalej: x₁<4 x₂<4 x₁−4<0 x₂−4<0 Stąd: x₁+x₂−8<0 i (x₁−4)(x₂−4)>0 Teraz tylko stosujesz wzory Viete'a.

Sampas : tak wiem z tym p to pomyłka

Sampas : juz rozumiem, dziękuję

Jolanta: wychodi mii m∊(−1, 1)