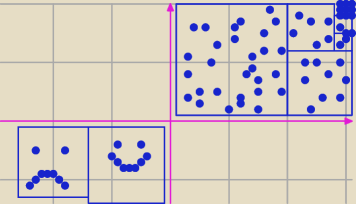
Zadania z funkcji dwóch zmiennych Damian#UDM: Funkcje dwóch zmiennych 1) Wyznacz dziedzinę funkcji

	1
f(x,y) =
	√xy

x*y>0 , czyli nierówność będzie spełniona gdy 1. x<0 i y<0 lub 2. x>0 i y>0 Czy dziedzina to będzie I oraz III ćwiartka układu współrzędnych?

ICSP: tak.

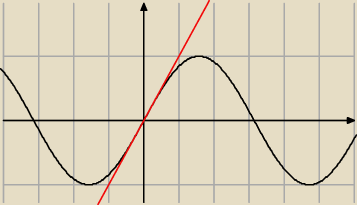
Damian#UDM: Super, dziękuję 2) Wyznacz dziedzinę funkcji f(x,y)=√x*siny x*siny≥0 , czyli nierówność będzie spełniona dla 1. x≥0 i y∊<2kπ, π+2kπ>, k∊C (zbiór liczb całkowitych) oraz 2. x≤0 i y∊<−π−2kπ, −2kπ>, k∊C Czy jest dobrze? Jak to zaznaczyć na osi układu współrzędnych?

ICSP: na osi może być trudno. To poziome pasy które będą się tak jakby stykać wierzchołkami na osi rzędnych.

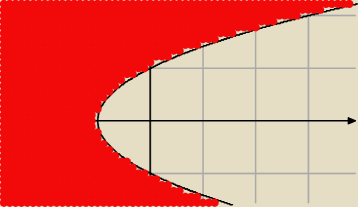
Damian#UDM: 3) Wyznaczyć dziedzinę funkcji f(x,y)=ln(y²−x−1) y²−x−1>0 x<y²−1

Damian#UDM: Rozumiem, dziękuję ICSP

Damian#UDM: https://drive.google.com/drive/folders/1lOY3xZ5i7vqtVIPiYGC5xKwt50mcL13x?usp=sharing O co chodzi w zadaniu 2. ? Na przykład zadanie 2.1

	δ2f		δ2f		δ2f
Nie wiem co oznacza ten zapis		*		=(		)2
	δx2		δy2		δxδy

Louie314: To są pochodne cząstkowe drugiego rzędu po zmiennej x i po zmiennej y.

Louie314: Tutaj przykład 2.1: https://prnt.sc/11x850z Dla reszty obliczamy podobnie. Mam nadzieję, że się nigdzie nie pomyliłem.

Damian#UDM: 3) Naszkicuj w układzie współrzędnych OXY zbiór punktów, w których funkcja f(x,y) = arctg(√y+x) spełnia nierówność

	δf		1		δf		1		δ2f
4√y*(		)2 +		*(		)2 <		*
	qy		y		qx		2y		δx2

Już mniejsza z tym szkicowaniem, jak to rozwiązać? Bo mi straszne wyniki wyszły

Louie314: Dobrze policzyłeś pochodne cząstkowe? Zobacz to, co zrobiłem powyżej.

Damian#UDM: Dobra, już wiem zrobiłem błąd przy podstawianiu do nierówności. Teraz ładnie wychodzi. Dziękuję Louie314 za pomoc