Deltoid
Kartofel : Dany jest deltoid o obwodzie 98, na którym można opisać okrąg. Niech 2α oznacza miarę
największego z kątów wewnętrznych tego deltoidu oraz tgα=−24/7. Oblicz promien okregu
opisanego na tym deltoidzie oraz promień okregu opisanego w ten deltoid.
22 kwi 23:57
Kartofel : Tam miało być tg2α=−24/7
22 kwi 23:58
chichi:
Pierwsza uwaga: w deltoidzie kąty między bokami różnej długości mają tę samą miarę oraz na
deltoidzie można opisać okrąg, stąd wynika, że te kąty są...?
23 kwi 00:28
Kartofel : α+γ=β+δ=180
23 kwi 00:45
figo:
R= 17,5
r=12
23 kwi 00:51
figo:
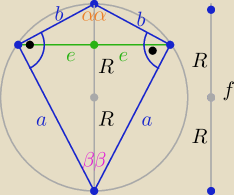
a+b=49
| | ab | |
Pr=2R*e i Pr=ab to e= |
| |
| | 2R | |
| | 2tgα | | 24 | |
tg2α= |
| = − |
| |
| | 1−tg2α | | 7 | |
12tg
2α−7tgα−12=0
wyznacz tgα >0 bo α −− kąt ostry
to z a+b=49 wyznacz a i b
a=28, b= 21
a
2+b
2=4R
2 ⇒ ......... R=....
to P
r= ...
| | P | |
ze wzoru P=rp r= |
| =... |
| | 49 | |
dokończ oblicznia
23 kwi 01:05
chichi:
Trochę się naliczyłem, ale potwierdzam wynik
23 kwi 01:11
chichi:
| | 2P | |
Można promień okręgu wpisanego też policzyć tak: r= |
| , gdzie P=ab, a L jest podane |
| | L | |
23 kwi 01:14
figo:
23 kwi 01:15
figo:
Mój "jęzor" ładniejszy
23 kwi 01:16
chichi:
| | sin(2x) | | 24 | | 24 | |
Ja się nieco wkopałem, bo liczyłem |
| =− |
| ⇒ sin(2x)=− |
| cos(2x) |
| | cos(2x) | | 7 | | 7 | |
| | 24 | | 7 | | 7 | | 4 | |
(− |
| cos(2x))2+cos2(2x)=1 ⇒ cos(2x)=− |
| ⇒ 1−2sin2(x)=− |
| ⇒ sin(x)= |
| |
| | 7 | | 25 | | 25 | | 5 | |
Ale reszta juz szybciutko
23 kwi 01:19
figo:
Można i tak
Ja jak widzę tg(2α) to stosuję gotowy wzór na tg(2α)
23 kwi 01:23
figo:
"dużo" ludzi na forum
23 kwi 01:25
chichi:
Wiesz co, ta jeż go zastosowałem, ale źle policzyłem deltę z równania 24tan
2(x)−14tan(x)−24=0,
wyszła brzydka, więc spróbowałem czego innego i wyszło, to już z przemęczenia.
Dziś od 8 rano do 15 zajęcia, po zajęciach nauka i forum aż dotychczas, wystarczy na dziś
23 kwi 01:35
chichi:
ta jeż → ja też, sama widzisz
23 kwi 01:36
figo:
Dobrej nocki, kolowych snów
23 kwi 01:44
figo:
Sorry
brakuje paru kolorowych literek ....
23 kwi 01:45
chichi:
Dziękuję i wzajemnie
23 kwi 01:49
Kartofel : Dziękuję wszystkim 😁
23 kwi 08:13