Równanie kwadratowe z parametrem
Cukrowy Ziemniaczek: Oblicz liczbę rozwiązań równania mx2+mx−1−2m=0 w zależności od parametru m∊R.
Mam problem z tym "m", które stoi przy x2. Kiedy obliczam deltę i np. zakładam sobie, że jest
ona większa od zera i otrzymuję jakieś wyniki dla m, nie wiem w którą stronę skierować ramiona
paraboli.
22 kwi 18:49
ICSP: Rozważ przypadki:
1o m = 0
2o m ≠ 0
Nie widzę za bardzo związku między skierowaniem ramion paraboli a ilością jej miejsc zerowych.
22 kwi 18:55
chichi:
(1) gdy m=0 mamy: −1=0 sprzeczne − brak rozwiązań
(2) gdy m≠0
Δ=m
2−4m(−1−2m)=m(9m+4)
| | 9 | |
Δ>0 ⇔ m(9m+4)>0 ⇔ m∊(−∞,− |
| )∪(0, +∞) − 2 rozw. |
| | 4 | |
| | 9 | |
Δ=0 ⇔ m(9m−4)=0 ⇔ m=0 − odrzucamy z (1) warunku ∨ m=− |
| − 1 rozw. |
| | 4 | |
| | 9 | | 9 | |
Δ<0 ⇔ m(9m+4)<0 ⇔ m∊(− |
| ,0) ∧ m=0 ⇒ m∊(− |
| ,0] − 0 rozw. |
| | 4 | | 4 | |
22 kwi 18:58
Cukrowy Ziemniaczek: No właśnie o ten moment mi chodzi:
| | 9 | |
Δ>0 ⇔ m(9m+4)>0 ⇔ m∊(−∞,− |
| )∪(0, +∞) − 2 rozw. |
| | 4 | |
| | 9 | |
Nie wiedziałem czy ma być tak, czy też m∊(− |
| ,0). |
| | 4 | |
Dlaczego tak?
22 kwi 19:03
chichi:
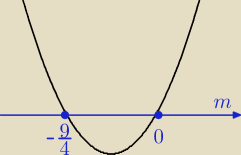
22 kwi 19:06
ICSP: rozwiązujesz nierówność kwadratową, ze względu na m:
m(9m+4)>0
9m2 + 4m > 0
współczynnik przy najwyższej potędze jest równy 9 > 0, więc parabola ma ramiona skierowane do
góry.
22 kwi 19:08
Cukrowy Ziemniaczek: Aha, matko. Bo ja mam patrzeć na 9 przy m2, a patrzyłem na m przy x2 i zastanawiałem się co
mam robić skoro nie znam znaku XD
Za dużo matmy na dziś XD Już ogarniam swoje nieogarnięcie, przepraszam, że zawróciłem głowę.
22 kwi 19:10
