help
dzonypieczony: Funkcja f(x)= x3+ax2+bx+1 ma w punkcie 1 x = 2 minimum lokalne równe (−7) .
Wyznacz wartość maksimum lokalnego funkcji f .
pomoże ktoś z tym ?
22 kwi 16:14
janek191:
f '(x) = 3 x
2 + 2a x + b
f '( 2) = 12 + 4 a + b = 0 ⇒ b = − 4a − 12
oraz
f( x) = x
3 + a x
2 −( 4 a + 12) x + 1
f(2) = − 7
8 + 4a − ( 8a + 24) + 1 = − 7
− 4 a − 8 = 0
a = − 2
b = − 4
więc
f(x) = x
3 −2 x
2 − 4 x + 1
Dokończ

22 kwi 16:20
janek191:
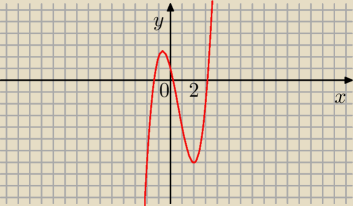
22 kwi 16:22
janek191:
f '(x) = 3 x
2 −4 x − 4 = 0
22 kwi 16:25
dzonypieczony: dzieki janek
22 kwi 19:47

