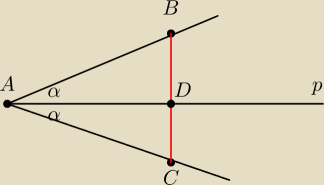
trojkaty 6latek: Na dowolnej prostej p obrano pewien punkt A i w tym punkcie zdudowano po obu stronach postej p dwa dowolne ale rowne sobie kąty. Na otrzymanych ramionach tych kątow odmierzono dwa dowolne ale rowne odcinki AB=ac .Punkty B i C polaczono odcinkien BC Udowodnic ze prosta p jest prostopadla do odcinka BC i dzieli go na polowy ΔADB≡ΔADC sa to trojakaty prostokatne ∡ADB=∡ADC=90^o ∡DAB=∡DAC z odmierzenia AB=AC z odmierzenia Wiec na podstawie cech kbk te trojkaty sa przystajace Z tego wynika ze ΔABc jest trojkatem rownoraniennym Prosta p jest dwusieczna kata BAC W trojkacie rownoraniennym dwusieczna jest prostopadle do podstawy i dzieli ja na polowy Teraz zauwazylem ze przystawanie tych trojkatow mozna bylo tez z cech B K B Dobrze ?

6latek:

Maciess: Jak uzasadnisz że są to trójkąty prostokątne?

6latek: Juz jestem . Maciess moze byc tak ? Skoro prosta BC laczy punkty BC ktore sa rownoodlegle od prostej p to oznacza ze prosta p jest symetralna odcinka BC

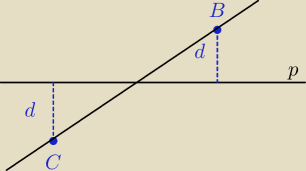
ite: tutaj również prosta BC łączy punkty BC, które są równoodlegle od prostej p

6latek: Dzien dobry ite Ale wtedy prosta p nie bedzie prostopadla do BC jak chca w zadaniu

ite: Dzień dobry! Maciess zapytał, na podstawie czego wyciągasz wniosek, że ΔADB≡ΔADC są to trójkąty prostokątne. Uzasadnienie z 11:55 nie jest wystarczające, żeby wykazać poprawność zapisu ∡ADB=∡ADC=90^o. Punkty B i C oraz prosta p z 12:10 również spełniają warunek, który podałeś ale narysowane proste nie są prostopadłe.

6latek: WIec jakie uzasadnienie byloby wystarczajace ?

ite: Myślę, że to będzie przejrzyste: ΔADB≡ΔADC \\ |AB|=|AC| z założenia, |<DAB|=|<DAC| z założenia, AD bok wspólny (czyli cecha bkb tak jak napisałeś) 1/ z tego wynika równość boków |BD|=|CD|, więc prosta p dzieli odcinek BC na połowy 2/ wynika również równość kątów |<ADB|=|<ADC|. Ich suma wynosi 180^o, więc miara każdego wynosi 90^o czyli prosta p jest prostopadła do odcinka BC

6latek: dziekuje