Punkt A = (2, -3) jest wierzchołkiem rombu ABCD o polu równym 300. Kck: Punkt A = (2, −3) jest wierzchołkiem rombu ABCD o polu równym 300. Punkt S = (3,4) jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu. Policzyłem współrzędne wierzchołka C które mi wyszły (4,11). Aby obliczyć współrzędne wierzchołka B miałem kilka pomysłów. Najpierw dowiedzieć się jaki współczynnik kierunkowy ma prosta AC, następnie napisać równanie prostej prostopadłej do tej prostej i przechodzącej przez punkt S. W ten sposób punkt B będzie leżał na tej prostej i będę mógł przyjąć jego oznaczenia jako B=(xb;−¹₇xb+³¹₇) (Przy czym nie mam pewności że nie ma tutaj błędu). Następnie chciałem albo przyrównać bok AB do boku BC, albo obliczyć |AS|, potem z Pitagorasa |AB| i przyrównać do wzoru na odległość punktów. Czy w ten sposób możliwe jest obliczenie wierzchołka B? Ponieważ wszystko wyliczyłem a wyniki wyszły mi niepoprawne.

chichi: Nie chce mi się sprawdzać Twojego rozwiązania teraz, zmęczony jestem, ale zaproponuje swoje: (1) Policz |AC|

	|AC||BD|
(2) Wyznacz długość drugiej przekątnej ze wzoru P=
	2

	|BD|
(3) Zaczep okrąg w punkcie S=(3,4) o promieniu r=
	2

	1		31
(4) Znajdź punkty wspólne okręgu z prostą o równaniu y=−		x+
	7		7

Kck: Na takie rozwiązanie bym nie wpadł ale nie bardzo rozumiem. Będzie to okrąg wpisany w romb czy opisany na rombie? Jeżeli wpisany to czy ^|BD|₂ na pewno będzie jego promieniem? A jeżeli opisany na rombie to czy ten romb nie musiałby być kwadratem?

6latek: napewno bedzie wpisany Kiedy mozna wpisac w czworokat okrag ? Gdzie lezy srodek okregu wpisanego w czworokat? czym sa przekatne w rombie ? Jesli sobie odpowiesz na te pytania watpliwosci znikna

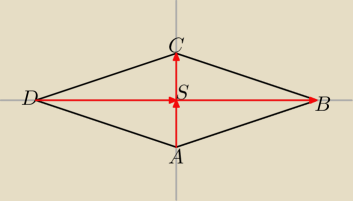
πach: Zaangażujemy wektory |AS| = √(3 − 2)² + (4 + 3)² = 5√2, 5√2 * |DB| = 300, |BD| = 30√2, |DS| = |SB| = 15√2 = 3|AS|, → → AS = [1, 7] = SC, C = (3 + 1, 4 + 7) = (4, 11) → SB = 3[7, −1] = [21, −3], B = (3 + 21, 4 − 3) = (24, 1), D = (3 − 21, 4 + 3) = (−18, 7)

6latek: Juz mialem pisac ze Pani Eta zrobi na wektorach .

πach: Nie jestem Panią Etą

6latek: Pani Eta ma teraz tyle nickow na π wiec tak pomyslem

Kck: Hmm... muszę przeanalizować to jutro bo teraz to czas na spanie. Ale wracając do początku. Czy moje sposoby też są poprawne i udałoby mi się wyliczyć z nich współrzędne wierzchołka B? Bo najprawdopodobniej na takie metody wpadłbym podczas pisania matury.

chichi: @6latek @Kck nie będzie ani wpisany, ani opisany... To tylko okrąg, do którego należą wierzchołki B i D, a znajdują się one w punktach przecięcia tegoż okręgu z prostą o równaniu

	1		31
y=−		x+		. Aczkolwiek polecam pomysł @πach, jest dużo szybszy
	7		7

πesio:

chaπ:

chichi: @6latek mogę zaczepić w punkcie S nieskończenie wiele okręgów, które nie będą ani wpisane, ani opisane na tym rombie. Jeżeli miałby być wpisany, to długość promienia musiałaby być równa

	h		|BD|
		, a nie		. Sam okrąg wpisany jest styczny do boków więc nie możliwe, aby
	2		2

jakakolwiek prosta miała punkty wspólne z tym okręgiem będące zarazem jakimikolwiek wierzchołkami rombu

Kck: W rozwiązaniu z wektorami nie rozumiem ostatniej linijki. Skąd się bierze [7, −1] i wszystko co dalej?

chichi: πach ciekawe kto się nabierze, że to nie Ty

chaπ:

chaπ: → → SC=AS= [ x_S−x_A, y_S−y_A] = [1,7]

πqś: Dobrej nocki Wszystkim

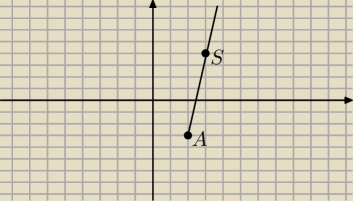
6latek: A=(2,−3) S=(3,4) a− prostej AS= 7

	1
stad a1=−
	7

Rownanie prostej prostopadlej do AS i przechodzacej przez S =(3,4)

	1		1		3		28		1		31
y=−		(x−3)+4= −		x+		+		= −		+		(liczylem w pamieci ale
	7		7		7		7		7		7

powinno byc oK

	1		31
Punkt B ktory bedzie lezal na tej prostej bedzie mial wspolrzedne B=(xB, −		xB+
	7		7

) Wyzej mamy obliczone ze |BD|= 30√2 stad polowa |BD|= 15√2 (bo przekatne sie polowia w rombie Wie odleglosc punktu B od punktu S wynosi 15√2 Wzor na odleglosc punktow

	1		31
√(3−x)2+( 4−(		x+		)2= 15√2
	7		7

	1		3
√(3−x)2+(−		x−		)2= 15√2 /2
	7		7

(3−x)²+(1/7x−3/7)²= 225*2=450 Obliczenia zmudne ale x=−18 lub x=24

	1		31
Stad y=−		*(−18)+		= U{18/7+31/7=7 stad B=(−18,7)
	7		7

	1		31
lub y=		*24+		= −1 stad B1= (24,−1)
	7		7

Mozna sprawdzic ze jesli B=(−18,7) to D=(24.−1) Jezeli B₁=(24,−1) to D=(−18,7) ze wzorow na srodek odcinka Duzo wiecej liczenia niz na wektorach wiec czas sie zaczac uczyc tych wektorow

6latek: Tak zrozumialem o co chodzi z tym okregiem . dziekuje

πqś: Łatwiej przekształcić równanie prostej : x= 31−7y B=(31−7y, y)

6latek: W sumie masz racje bo wtedy pozbedziemy sie ułamków Ułamki tez sa dobre ,bo mozna pól flaszki podzielic na dwóch a nie cała na dwoch

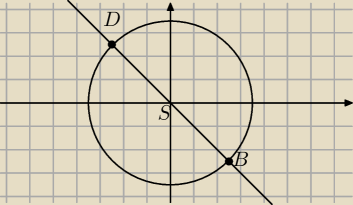
6latek: Chodzi o taka sytuacje z tym okregiem