Pole pewnego trójkąta
matma_podstawa: Czy zadanie 21. ze strony:
https://zdajmyto.pl/arkusze/4
Polega na zgadnięciu, że trójkąt jest prostokątny?
Treść:
Ile jest równe pole pewnego trójkąta o bokach długości 6,8,10?
20 kwi 22:38
ICSP: Nie zgadnięciu, a sprawdzeniu.
20 kwi 22:41
Jolanta: Twierdzenie Pitagorasa wykorzystaj
20 kwi 22:42
ABC: wzorem Herona jedziesz i masz w d.... czy jest prostokątny czy nie
20 kwi 22:45
Jolanta: Jezeli chcesz sprawdzić czzy jest prostokątny .Jeżeli chcesz pole wyliczyc to ze wzoru Herona
20 kwi 22:46
matma_podstawa: W takim razie załóżmy, że zadanie nie jest z serii "A,B,C,D".
Jak wtedy formalnie to zapisać?
Czy napisanie:
Trójkąt jest prostokątny, ponieważ spełnia tw. Pitagorasa:
62 + 82 = 102
jest wystarczającym uzasadnieniem?
20 kwi 22:48
matma_podstawa: Faktycznie wzór Herona! Dzięki!
20 kwi 22:49
ICSP: Stosuj lepiej wzór Herona bo to uzasadnienie to woła o pomstę do nieba.
20 kwi 22:50
Jolanta: Mozesz 6
2+8
2=10
2 trójkat jest prostokątny
20 kwi 22:52
Jolanta: ICSP dlaczego?
20 kwi 22:53
ICSP: Znasz treść twierdzenia Pitagorasa?
Jakie tam są założenia a jaka teza?
20 kwi 22:55
πesio:
W zadaniu testowym chodzi zakreślenie poprawnej odpowiedzi!
P=24
i po ptokach
20 kwi 23:06
ABC: jeżeli chce udowadniać że trójkąt jest prostokątny , to z twierdzenia odwrotnego do
tw.Pitagorasa,
które szczęśliwym trafem okazuje się być prawdziwe
20 kwi 23:07
πesio:
@
ICSP możesz liczyć to pole nawet za pomocą całki
20 kwi 23:07
ICSP: Dobrze, że nie dają takich otwartych bo byłby problem
Wzór Herona załatwia sprawę.
Jeżeli nie musimy opisywać rozwiązania to lepiej tego nie róbmy.
20 kwi 23:08
πesio:
Nie przesadzaj
20 kwi 23:09
ABC:
nie egzageruj Mirmiłku jak to było w moim ulubionym komiksie Kajko i Kokosz
20 kwi 23:10
Jolanta: Pamietam,że przy zadaniach; Sprawdz czy trójkąt jest prostokątny' robi sie to za pomoca
twierdzenia Pitagorasa
Tak sie dzieci uczą w szkole
20 kwi 23:10
πesio:
@
ICSP
Oblicz pole trójkąta o bokach długości : 15,30,15
20 kwi 23:10
Jolanta: tzn odwrotnego do tw Pitagorasa
20 kwi 23:12
πesio:
Dobrze
Jolanta 
20 kwi 23:12
Jolanta:
20 kwi 23:18
6latek:
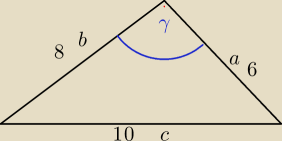
Twierdzenie
jezeli w trojkacie γ<90
o to c
2<a
2+b
2
jezeli w trojkacie γ=90
o to c
2=a
2+b
2
jezeli w trojkacie γ>90
o to c
2>a
2+b
2
Twierdzenie odwrotne to tego twierdzenia takze jest prawdziwe
Dobrze takze jest pamietac ze trojkąt o bokach 3,4 5 a takze o bokach 6,8 10 jest prostokatny
i wiele innych
20 kwi 23:33
matma_podstawa: Dziękuję!
21 kwi 15:00
Mila:
Zadanie możesz rozwiązać bez tej wiedzy, że Δ o bokach 6,8,10 jest Δprostokątnym.
Jednak uczeń, który poznał tw. Pitagorasa powinien to wiedzieć, to znacznie ułatwia
rozwiązanie.
W wielu przypadkach , gdy dane są boki Δ warto sprawdzić, czy to może być Δ prostokątny.
21 kwi 18:20
6latek:
21 kwi 22:01