nierówność z wartością bezwzględną
Rafał: całość w wartości bezwzględnej
x2 − 5x +3 /x2 − 1 < 1
jestem w momencie
(−5x +4)(x2 −1) <0 i (2x2 − 5x +2)(x2−1) <0
teraz do postaci iloczynowych i wykres wielomianu?
20 kwi 09:55
6latek: To samo dziedzina
Mozesz tak
korzystasz z tego ze
|x|<a⇔x<a i x>−a
i
masz o rozwiazania dwie nierownosci
20 kwi 10:18
6latek: Mozna to rozwiazac jeszcze inaczej ale nie bede Ci juz mieszal

20 kwi 10:20
Rafał: okej, czyli dla tej pierwszej otrzymuję
(−5x+4)(x+1)(x+1) < 0
i dla drugiej
2(x−0,5)(x−2)(x1)(x−1) >0
o to chodzi?
20 kwi 10:23
Rafał: 2 (x−0,5)(x−2)(x+1)(x−1) > 0 (wkradł się wyżej błąd)
20 kwi 10:24
6latek: Pierwsza zapisana zle
(−5x+4)(x+1)(x−1)<0
albo rownowaznie
(5x−4)(x+1)(x−1)>0
Druga nie sprawdzalem
20 kwi 10:31
6latek: druga
| x2−5x+3 | | x2−1 | |
| + |
| >0 |
| x2−1 | | x2−1 | |
rownowaznie
2(x−2)(x−0,5)(x+1)(x−1)>0 masz dobrze
20 kwi 10:39
Rafał: tak tak, czyli mamy x = 4/5, x = −1, x = 1. są to pierwiastki jednokrotne i teraz jak rysujemy
to od prawej strony od góry czy od dołu przez to że było −5x?
20 kwi 10:42
6latek: Od dolu bo (−x)*x*x= −x3
20 kwi 10:43
ICSP: | | x2 − 5x + 3 | |
| |
| | < 1 dla x ≠ 1 ∧ x ≠ −1 |
| | x2 − 1 | |
(x
2 − 5x + 3 + x
2 − 1)(x
2 − 5x + 3 − x
2 + 1) < 0
(2x
2 − 5x + 2)(5x − 4) > 0
| | 1 | |
(x−2)(x − |
| )(5x−4) > 0 |
| | 2 | |
| | 1 | | 4 | |
x ∊ ( |
| , |
| ) ∪ (2 , ∞) |
| | 2 | | 5 | |
20 kwi 10:52
Rafał: okej czyli z tej strony mamy (−1, 0,8) suma (1, ∞)
20 kwi 10:53
Rafał: z drugiej strony (−∞,−1) suma (0,5;1) suma (2, ∞)
20 kwi 10:56
6latek: Teraz rozwiazanie drugiej nierownosci
20 kwi 10:56
Rafał: i teraz jak to razem przedstawić ?
20 kwi 10:56
6latek: Teraz te rozwiazania na os liczbowa i czesc wspolna
Inny sposob pokazal ICSP .
20 kwi 10:58
6latek:
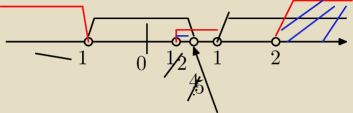
20 kwi 11:04
Rafał: dzięki bardzo !
20 kwi 11:05
6latek: Na zdrowie


20 kwi 11:06



