planimetria kbs: w trójkącie prostokątnym ABC o kącie prostym w wierzchołku b , środkowe AD I BE są prostopadłe . Wyznacz tangens kąta ACB

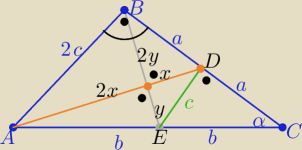
πesio: Można tak: 4x²+y²=b² i x²+4y²=a² +−−−−−−−−−−−−−−−−− 5(x²+y²)=a²+b² 5c²=a²+b² / : a²≠0

	1		1		cos2α+sin2α+cos2α
5tg2α=1+		1+		=		=2+tg2α
	cos2α		cos2α		cos2α

więc 4tg²α=2 α −− kąt ostry

	√2
zatem tgα=
	2

========

kbs: Dlaczego 4x² + y² =b², a nie 2x²

kbs: Nie było pytania już widzę

πesio: Można jeszcze tak: 5c²=a²+b² i w ΔDEC: c²=b²−a² odejmując stronami

	c		1
4c2=2a2 ⇒ (		)2=
	a		2

	1
to tg2α=		i α −−ostry
	2

	√2
tgα=
	2

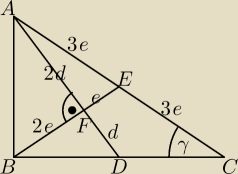πach: ΔAFE: 4d² + e² = 9e², stąd 4d² = 8e² i d² = 2e² ΔABF: |AB| = √ 4d² + 4e² = √ 12e² ΔBDF: |BD| = √ d² + 4e² = √ 6e² i |BD| = |DC|

	|AB|		√ 12e2		√2
tgγ =		=		=
	|BC|		2√ 6e2		2

chichi: Robiłem tym sposobem co @πach

chaπ: