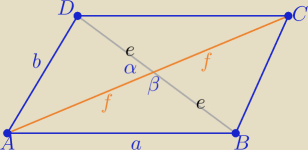
W równoległoboku fifi: W równoległoboku o bokach długości a i b, gdzie a > b, kąt między przekątnymi ma miarę α, α ∈ (0°, 90°). Wykaż, że pole P tego równoległoboku jest równe 1/2(a2 − b2) · tgα.

πesio:

	P
P(ABCD)=P= 2fe sinα ⇒ 2fe=
	sinα

β>α i β=180^o−α to cosβ= −cosα dwa razy z tw. cosinusów : a²=f²+e²+ 2fecosα i b²=f²+e²−2fecosα − −−−−−−−−−−−−−−−−−−−−−

	2P
a2−b2=4fecosα =		*cosα
	sinα

	1
to P=		(a2−b2)*tgα
	2

=================== c.n.w.