matematykaszkolna.pl
Jak określić, czy funkcja f będzie rosnąca dla x>1? ks: Jak określić, czy funkcja f będzie rosnąca dla x>1?
 x4+2x2−4x+1 (x−1)(x3+x2+3x−1) 
Pochodna jest równa f'(x)=
=
 (x2+1)2 (x2+1)2 
Co z miejscem/miejscami zerowymi x3+x2+3x−1?
19 kwi 15:35
Jerzy: A po co ci miejsca zerowe ? Gołym okiem widać ,że dla x > 0 pochodna jest dodatnia , bo x − 1 > 0 , x3 + x2 + 3x − 1> 0 oraz (x2 + 1)2 > 0
19 kwi 15:47
ks: Nie wiem skąd wiadomo, że x3 + x2 + 3x − 1 > 0.
19 kwi 15:50
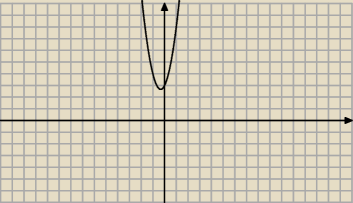
Jerzy: rysunek Popatrz na wykres pochodnej drugiego nawiasu, przyjmuje tylko wartości dodatnie.
19 kwi 15:55
Jerzy: To znaczy ściślej dla x =1 pochodna ma wartość 7, a dalej tylko rośnie , czyli nawias jest dodatni.
19 kwi 16:02
Jerzy: A może jeszcze inaczej. Pochodna drugiego nawiasu jest zawsze dodatnia, czyli funkcja w drugim nawiasie jest stale rosnąca.Dla x = 1 przyjmuje wartość 4 , czyli dla x > 1 musi być dodatnia
19 kwi 16:13
ks: Dziękuję
19 kwi 16:17
Mariusz: Jerzy wprowadza cię w błąd Wielomian stopnia nieparzystego o współczynnikach rzeczywistych ma co najmniej jeden pierwiastek rzeczywisty
19 kwi 16:21
wredulus_pospolitus: @Mariusz ... nie spojrzałeś na warunek: x > 1 a w tym przedziale zachodzi x3 + x2 + 3x − 1> 0
19 kwi 16:27
Jerzy: @Mariusz,czytaj uważnie treść zadania.Nie wprowadziłem autora postu w błąd,jak twierdzisz.
19 kwi 16:45
Mariusz: Chcesz wiedzieć jak rozłożyć ten wielomian trzeciego stopnia ? W(x)=x3+x2+3x−1
 1 
Najpierw przedstawiasz W(x) w postaci sumy potęg dwumianu (x+
)
 3 
 1 1 1 
(x+
)3=x3+x2+
x+
 3 3 27 
 1 8 1 1 1 8 8 
(x+
)3+
(x+
)=(x3+x2+
x+
)+
x+
 3 3 3 3 27 3 9 
 1 8 1 25 
(x+
)3+
(x+
)=x3+x2+3x+
 3 3 3 27 
 1 8 1 52 25 52 
(x+
)3+
(x+
)−
=x3+x2+3x+
−
 3 3 3 27 27 27 
 1 8 1 52 
(x+
)3+
(x+
)−
=x3+x2+3x−1
 3 3 3 27 
 1 
y=x+
 3 
 8 52 
y3+
y−
=0
 3 27 
Teraz masz takie możliwości Podstawienie y=u+v albo przekształcenie Vieta
 8 
y2+yz=
 9 
 8 52 
y3+
y−
=0
 3 27 
y=u+v
 8 52 
(u+v)3+
(u+v)−
=0
 3 27 
 8 52 
u3+3u2v+3uv2+v3+
(u+v)−
=0
 3 27 
 52 8 
u3+v3−
+3(u+v)uv+
(u+v)=0
 27 3 
 52 8 
u3+v3−
+3(u+v)(uv+
)=0
 27 9 
 52 
u3+v3−
=0
 27 
 8 
3(u+v)(uv+
)=0
 9 
 52 
u3+v3=
 27 
 8 
uv+
=0
 9 
 52 
u3+v3=
 27 
 8 
uv=−
 9 
 52 
u3+v3=
 27 
 512 
u3v3=−
 729 
 52 512 
t2−
t−
=0
 27 729 
 26 676 512 
(t−
)2−
−
=0
 27 729 729 
 26 1188 
(t−
)2−
 27 727 
 26−6√33 26+6√33 
(t−
)(t−
)=0
 27 27 
 1 
y=
(3√26−6√33+3√26+6√33)
 3 
 1 1 
x+
=
(3√26−6√33+3√26+6√33)
 3 3 
 1 
x=
(3√26−6√33+3√26+6√33−1)
 3 
Znalazłem ten pierwiastek i okazało się że jednak jest mniejszy od jedynki
19 kwi 16:48
Jerzy: A do czego są potrzebne miejsca zerowe w tym zadaniu ?
19 kwi 17:02
ks: Można wtedy naszkicować wykres pochodnej i określić znak, ale teraz widzę że można zauważyć że wielomian jest większy od zera dla x>1 co jest prostsze
19 kwi 17:14
Jerzy: I to ci wyjaśniłem 16:13
19 kwi 17:27
wredulus_pospolitus: @Mariusz ... i po cholerę mu ten pierwiastek? Wystarczy spojrzeć na ten wielomian, aby szybko wywnioskować, że pierwiastek nie należy do rozpatrywanego przedziału, ewentualnie 'dla pewności' można policzyć pochodną i wykazać, że f(x) = x3 + x2 + 3x − 1 jest funkcją rosnącą w tymże przedziale + f(1) = 4 > 0
19 kwi 20:30