Geometria cmods: Dany jest trójkąt o wierzchołkach A=(−6,2) B=(4,−1) C=(−1, −4) Oblicz długości środkowych AD BE CF oraz współrzędne środka ciężkości tego trójkąta Bardzo Bardzo proszę o pomoc

janek191:

	3		−5
D = (		,		)
	2		2

	7
E = ( −		, −1 )
	2

	1
F = ( −1,		)
	2

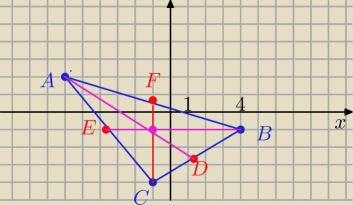
Teraz odlicz długości odcinków : AD, BE, CF Np. I EB I = 4 − ( − 3,5) = 7,5 I CF I = 0,5 − ( − 4) = 4,5 itd.

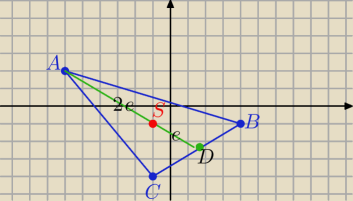
apanaczi: Łatwiej tak: Środek ciężkości trójkata , to punkt przecięcia środkowych S(x_S,y_S)

	xA+xB+xC		yA+yB+yC
xS=		i yS=		( wzór masz w karcie wzorów
	3		3

S(−1,−1) środkowe dzielą się w stosunku 2:1 licząc od wierzchołka to

	3
|AD|=		|AS| , |AS|=√(xS−xA)2+(yS−yA)2= .....√34
	2

	3√34
|AD|
	2

=========== pozstałe analogicznie ..........